科普 | 默克尔树的基础数据结构

本文主要介绍了默克尔树的基础数据结构，以及默克尔树相关的应用延伸的起点。

默克尔树简介

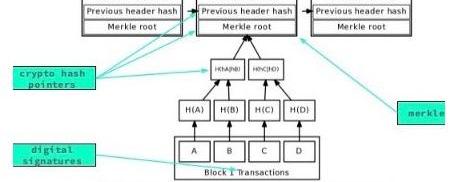
本文主要介绍了默克尔树的基础数据结构，以及默克尔树相关的应用延伸的起点。

在Coursera平台的比特币和加密货币技术课程中，作者学习了如何使用基于哈希的数据结构来验证P2P网络系统中数据完整性的基础知识。该课程中提到的核心数据结构之一是默克尔树，它存在于比特币区块链中，以一种非常有效地节省空间和时间的方式，来帮助验证交易的存在(本文后面会详细介绍!)。作者深入研究了默克尔树，意识到这个数据结构实际上是多么丰富的，所以决定写一篇默克尔树学习笔记。

美国说唱歌手Megan Thee Stallion与Cash App合作发布比特币科普视频:美国说唱歌手Megan Thee Stallion与由Square开发的移动支付服务Cash App合作发布了一段名为“Bitcoin for Hotties”的视频。该视频从她的角度解释了什么是比特币，为什么比特币有价值等内容。Megan Thee Stallion在Instagram上拥有超过2410万粉丝，在 Twitter上拥有640万粉丝。（Bitcoin News）[2021/8/8 1:41:10]

默克尔树解说

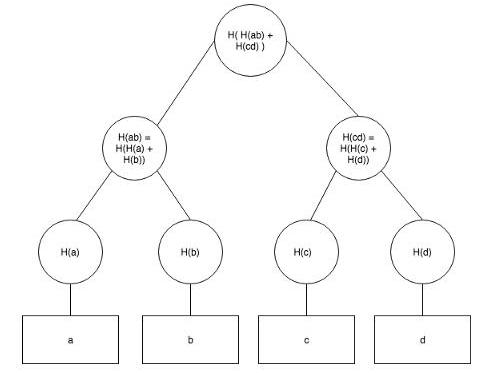
默克尔树构建完成后，看起来是这样：

欧科云链集团正式启动区块链科普行动“星途计划”:欧科云链集团于4月26日，正式宣布启动了区块链科普行动——“星途计划”，行动包括将在全国范围展开系列沙龙，加大力度推进区块链科普进机关、进国企、进校园等，联合政府部门、行业协会等共同构建起更加完善和有效的区块链科普教育生态，与此同时，直击区块链科普现存痛点，推出简单易懂的“秒懂区块链”公益短视频课。

该计划旨在全维度推动社会建立对产业更清晰的认知，与“鲲鹏计划”一道助力数字经济及区块链产业本身健康发展夯实“人才”和“产业认知”两大基础。[2021/4/26 20:59:37]

和H，如果没有缩写的话，根哈希也可以为H+H）+H+H）））

a、b、c、d是一些数据元素，H是哈希函数。如果你不是很了解哈希函数，可以把它理解为数据块的“数据指纹”，Hash是一个把任意长度的数据映射成固定长度数据的函数，而根据Hash值反推原始输入数据的特征是几乎不可能的。每个节点都是通过哈希运算父节点得到的，默克尔树的常见结构是二叉树，但也有非二叉树结构的，比如以太坊平上默克尔树。本文只讨论这种最常见的二叉树结构。

人大附中物理老师李永乐科普拜占庭将军问题和区块链:5月14日，人大附中物理老师、科普视频网红李永乐在其公众号发布视频《拜占庭将军问题是什么？区块链如何防范恶意节点？》。李永乐老师在视频中对拜占庭将军问题和区块链进行了讲解，他表示，拜占庭将军问题本质上指的是，在分布式计算机网络中，如果存在故障和恶意节点，是否能够保持正常节点的网络一致性问题。在近40年的时间里，人们提出了许多方案解决这一问题，称为拜占庭容错法。例如兰波特自己提出了口头协议、书面协议法，后来有人提出了实用拜占庭容错PBFT算法，在2008年，中本聪发明比特币后，人们又设想了通过区块链的方法解决这一问题。区块链通过算力证明来保持账本的一致性，也就是必须计算数学题，才能得到记账的权力，其他人对这个记账结果进行验证，如果是对的，就认可你的结果。与拜占庭问题比起来，就增加了叛徒的成本。[2020/5/14]

自下而上通过哈希运算相同高度的节点，直至生成默克尔树根节点。在生成默克尔树的时候，如果存在单个叶子节点无法匹配成对，就需要特殊处理这个情况，除此之外，树的构造非常简单。

动态 | 币安科普MimbleWimble算法:币安官方推特今日发布隐私算法Mimblewimble的科普贴，在下方留言区大量网友留言猜测是否是基于 Mimblewimble算法的隐私币Grin或者Beam即将登陆币安交易所，其中猜测Grin的呼声更高。[2019/9/2]

默克尔树构建完成后，就可以在O(logn)时间内使用根哈希对叶子进行验证，验证工作是通过重新创建包含从根到被验证的数据段进行的。在上面的例子中，如果想要验证c，那么就需要得到H和H+H）。数据c哈希后得到H，再将H与H进行哈希运算，然后将H与H在进行哈希运算，得到一个最后的哈希值，如果这个哈希值与根哈希相同，则说明c确实是默克尔树中数据的一部分。

在BT下载等情况下，是由另一方提供数据c，H和H+H）的，如果你担心这种方法的安全性，请记住在一个哈希函数上不可能找到e值使得H=H。这意味着只要根哈希是正确的，其他人很难作假他们提供的数据。

声音 | 火星人朋友圈科普RAM:火星人在朋友圈发文称，“什么是RAM？简单来说就是EOS这个国家的土地，所有的经济行为都离不开土地。只要EOS的BP们能投票形成一个稳定的供给预期，并且不改变目前的Bancor算法，那么RAM后续的价格有可能会像北上广深的房价走势。房价下跌不行，房价过快上涨也不行，EOS的生态越来越像某国了，真有意思。”[2018/7/6]

输出某些数据的验证路径和重新创建通向默克尔树根的分支一样简单。在数字签名方案中使用默克尔树时，验证整个默克尔树及其各个叶子节点自身的数据就很重要，并且这实际上是可以在O(logn)时间内完成。有一些更高级的算法是可以完成这一输出过程的。

默克尔树的执行方法

下图是完整版本的代码，作者将会在这里解释创建和验证默克尔树的方法。注意build_tree和_audit方法都是来自较大类的实例方法。

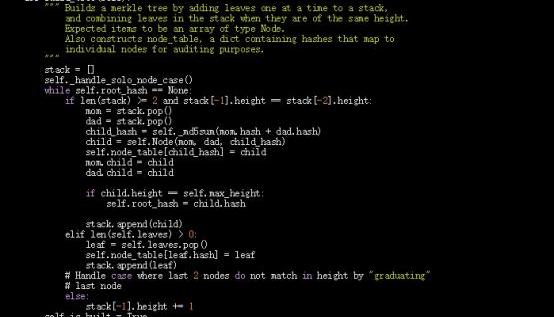
构建树的方法是将叶子添加到堆栈中，并检查堆栈中的前两个节点是否具有相同的高度。当高度相同时，节点有一个“子值”(两个节点哈希值相连后的再次哈希值)，当高度不同时，一个新节点会追加到堆栈中。当最后两个节点高度不同时，需要处理这种边缘情况。

上面的方法在单节点情况下会失败，因为不满足任何条件，所以有一个小方法来处理完整性。

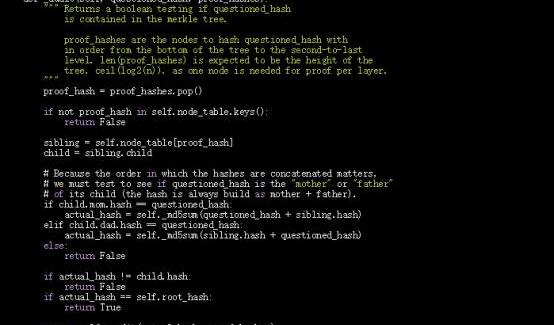
上图是本文要解释的验证过程。公开验证方法会检查一些先决条件，这就是为什么大部分逻辑放在这个私人版本中的原因。

默克尔树的应用

默克尔树在区块链中应用，近年来引起了人们的广泛关注。在许多P2P网络系统中(不仅仅是区块链)，个人需要能够从不受信任的一方获取数据，并证明对方发送给他们的内容是他们想要的真实内容。BT文件(种子文件)就是一个例子：当你下载一个BT文件时，你会收到别人在网上“播种”的BT文件，但是你怎么能确定这些文件真的，是你要下载的内容，而不是垃圾或恶意软件呢?默克尔树可以对从对方接收到的数据进行身份验证，以解决这个信任问题。

类似的问题也适用于像比特币和以太坊这样的加密货币：如果有人声称另一个同行在交易中向他们支付了费用，那么网络上的一个节点如何验证交易是否真的发生了呢?一种方法是，节点可以存储曾经发生过的完整交易历史记录，但是，就节点的时间和空间成本而言，这是不现实的。默克尔树提供了一种解决方案，可以为网络上的节点节省时间和空间。通过每个区块中的交易数据创建默克尔树，可以在O(logn)时间内审计交易。此外，它为一些比特币客户端提供了新的解决方案，可以节省空间，只存储默克尔树根，不需要存储历史每一笔交易，这创造了巨大的价值!

除了区块链和BT下载，默克尔树还能在任何需要有效检测不一致性的系统中被应用:

证书颁发机构(CAs)使用默克尔树作为证书透明性的一种方法。在这里，公钥私钥对被视为默克尔树的叶子。这是CAs用来防止某个CA可能耍无赖并试图在某个领域的所有者不知道证书的情况下对该领域的证书进行认证的一种机制。

高度可伸缩的数据库，如ApacheCassandra和DynamoDB，处理网络上复制数据库的故障。这个过程被称为“反熵”，ApacheCassandra博客和AmazonDynamoDB论文对其进行了较为深入的描述。

RSA的数字签名替代品，在这种情况下，默克尔树的根充当公钥，单个节点用作一次性签名。最近，人们做了更多的工作来推进这种技术，因为理论上它可以抵抗量子计算攻击(和RSA不一样，默克尔树为当今大多数公钥密码术提供了支持)。

默克尔树的应用确实很多，在任何特定领域的默克尔树应用都是需要长篇大论来论述的，在这里我们只做简单的介绍。

原文：https://hackernoon.com/merkle-tree-introduction-4c44250e2da7

稿源：https://first.vip/shareNews?id=2130&uid=1

标签：区块链比特币CASMBL以下哪项不是区块链目前的分类比特币套现很难吗Lilith CashMBLOX币

币安app官方下载最新版热门资讯