技术入门 | 深入理解零知识证明算法之Zk-stark：Low Degree Testing

前言

本系列的第二篇文章，以超市收据为例，描述了Arithmetization的具体过程。本文将以另外一个例子为基础，在回顾Arithmetization过程的同时，将内容引申到多项式的LDT过程。

新的实例

AliceClaim：“我有1000,000个数，他们都在范围内”。为了方便验证者Bob验证，Alice首先要对Claim进行Arithmetization转换。过程如下图1所示(图中：黑色箭头代表主流程，红色箭头代表附加说明信息，黄色圈对应下面详细说明的索引)

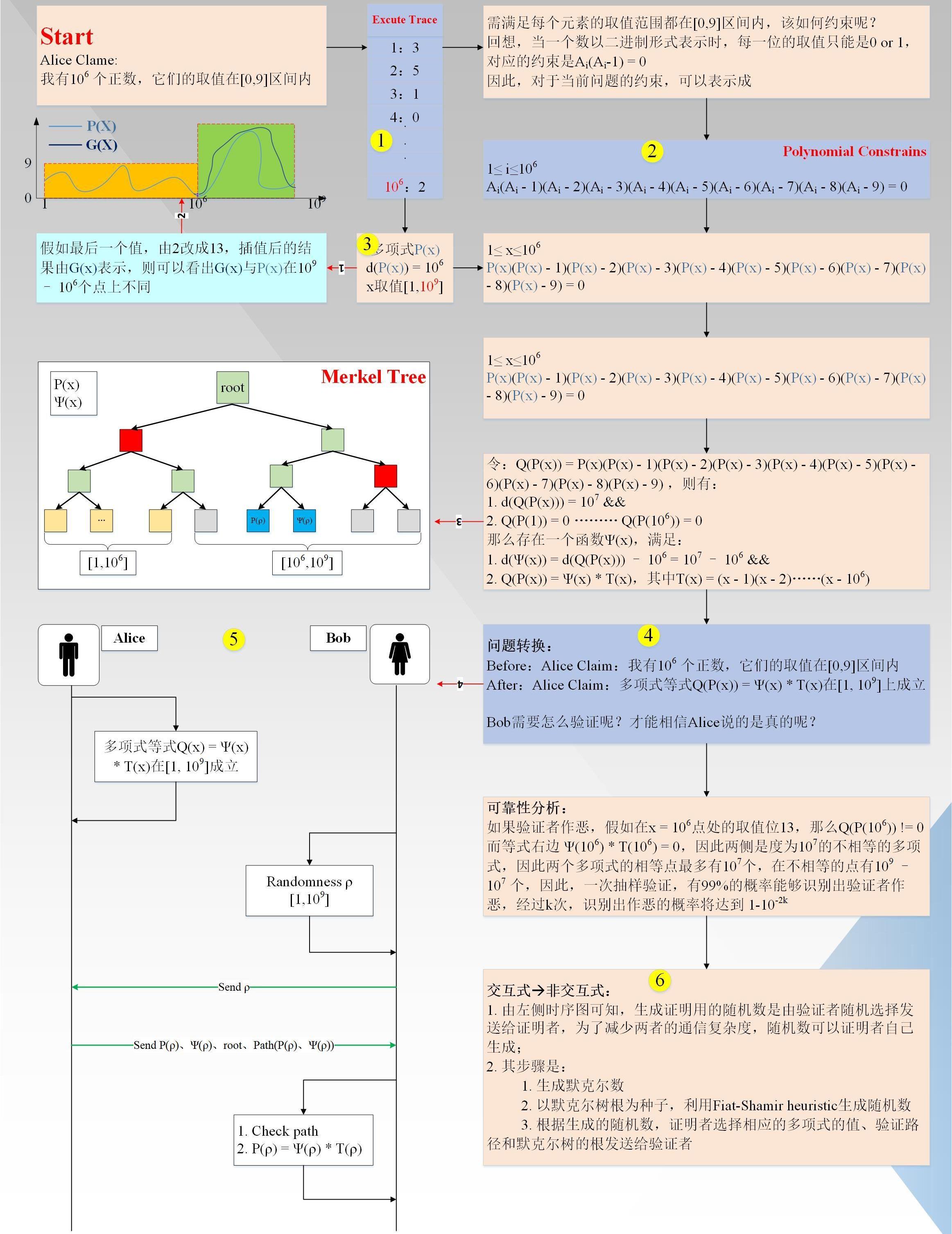
下面具体说明一下对应流程：

首先生成执行轨迹(EXCUTETRACE)，事实上，它是一张表，总共有1000,000行；

生成多项式约束(PolynomialConstrains)，多项式约束满足执行轨迹的每一行(个人理解：步骤1，2没有一定的先后依赖关系，只是习惯上先生成执行轨迹，再生成约束多项式)；

对执行轨迹进行插值，得到一个度小于1000,000的多项式P(x)、x取值，并计算更多点上的值，x取值范围扩大到(Reed-Solomen系统编码)；假如，证明者有一个值不在范围内(图中红线1/2所示)，假如就是第1000,000个点，它实际的值是13，大于9，其插值后的曲线G(x)如图所示，图中P(x)为有效曲线，G(x)为无效曲线。可以看出，两条曲线在变量x取值范围内，最多有1000,000个交点，即有1000,000,000-1000,000个点不同，这很重要。

将插值后的多项式P(x)和多项式约束进行组合变换，最终得到的形式为：

动态 | Mphasis与QEDIT签署协议 以提供基于区块链的增强隐私技术解决方案:信息技术解决方案提供商Mphasis周四宣布与QEDIT建立合作伙伴关系，为企业提供基于区块链的隐私增强技术解决方案。（Moneycontrol）[2020/1/23]

Q(P(x))=Ψ(x)*T(x)，其中T(x)=(x-1)(x-2)……(x-1000,000)，x取值

其中，d(Q(P(x)))=10,000,000、d(Ψ(x))=10,000,000-1000,000、d(T(x))=1000,000；

至此，问题就转化成了，Alice宣称“多项式等式在变量x取值范围内成立”的问题。那么验证者Bob该如何验证呢？具体过程如下：

证明者Alice在本地计算多项式P(x)、Ψ(x)在所有点上的取值，对！从1至1000,000,000，并形成一个默克尔树；

验证者Bob随机的从内选取一个值ρ，并发送给证明者Alice，要求其返回对应的信息；

证明者Alice返回P(ρ)、Ψ(ρ)、root、AuthorizedPath(P(ρ)、Ψ(ρ))给验证者Bob；

验证者Bob首先根据默克尔树验证路径验证值P(ρ)、Ψ(ρ)的有效性，然后等式Q(P(ρ))=Ψ(ρ)*T(ρ)，如果成立，则验证通过；

完整性分析：如果验证者Alice是诚实的，那么等式Q(P(x))一定会被目标多项式T(x)整除，因此必定存在一个d(Ψ(x))=d(Q(P(x)))-d(T(x))的多项式Ψ(x)，满足Q(P(x))=Ψ(x)*T(x)，因此对于任意的x，取值在之间，等式都会成立；

可靠性分析：如果验证者Alice是不诚实的，即类似于步骤3里的假设，在x=1000,000上，P(x)的取值为13，那么Q(P(1000,000))!=0，但是等式右边，T(1000,000)=0，因此Q(P(x))!=Ψ(x)*T(x)，即等式两边是不相等的多项式，其交点最多有10,000,000个，因此通过一次随机选取，其验证通过的概率仅为10,000,000/1000,000,000=1/100=0.01，经过k次验证，其验证通过的概率仅是1-10(^-2k)；

声音 | 分析师Mati：长期看好XRP因其技术好、团队强大等原因:推特网友提问“是什么让你长期看好XRP”，分析师Mati Greenspan表示，“好技术、强大的团队、可能是唯一一个定期与金融机构达成交易的加密项目。”[2019/12/31]

上述的验证过程为交互式的，如果是非交互式的，可以利用Fiat-Shamirheuristic进行变换，以默克尔树的根作为随机源，生成要查询的随机点；

LDT

我们忽略了一种攻击方式，即针对每一个数x，证明者都随机生成p，然后根据Ψ(x)=Q(p)/T(x)，这些点不在任何一个度小于1000,000的多项式上，但是可以通过验证者验证。如下图2所示：

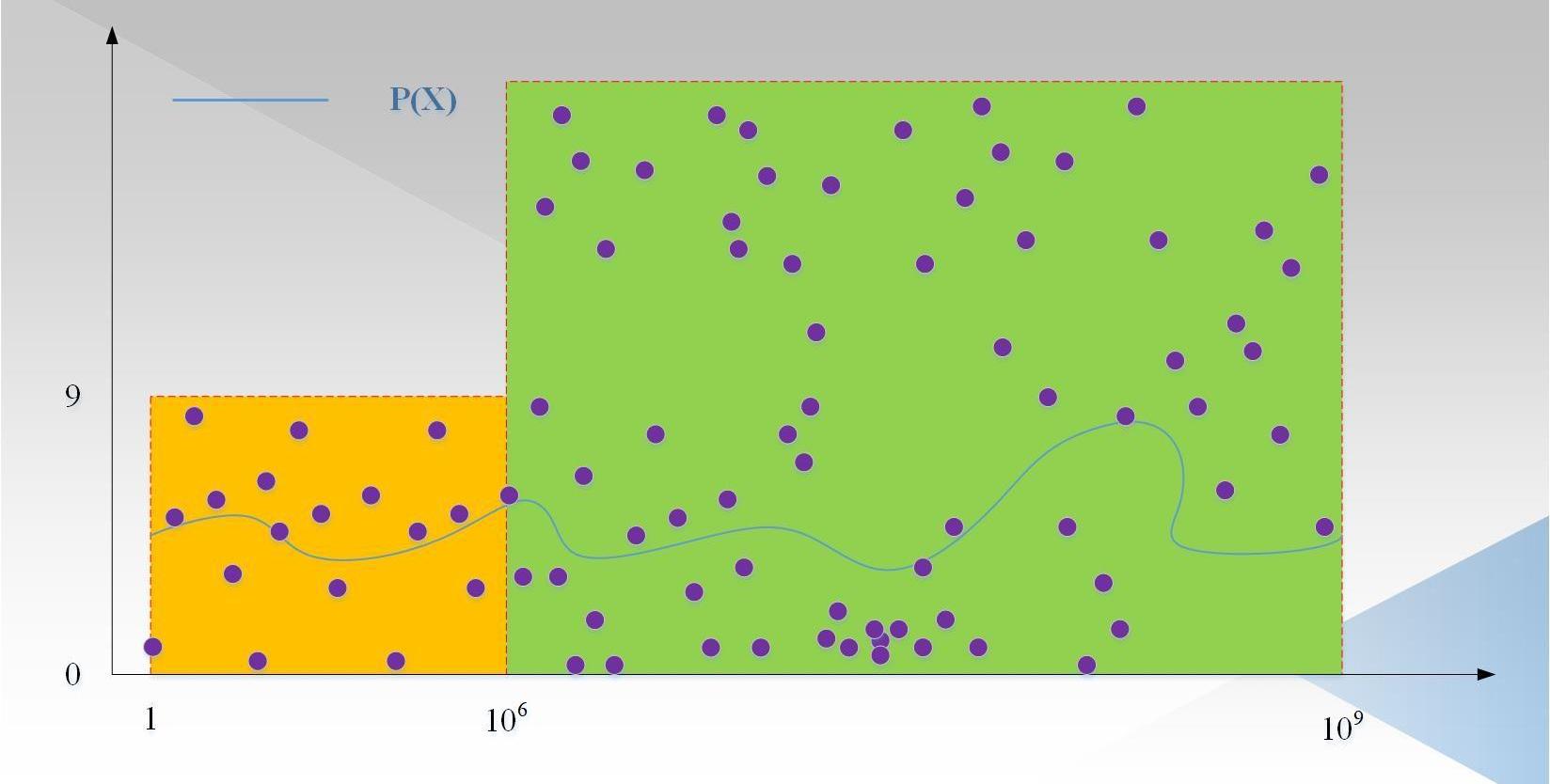
图中：紫色的点为随机生成的点p，这些点大概率不在一个度小于1000,000的多项式上(事实上，可以不考虑前1000,000个点，因为验证者只会从范围内取值)。因为即使选择1000,000个点插值出一个度小于1000,000的多项式，也不能保证其他的点在这个多项式上，因为其他的点是随机生成的。因此，需要有一种方式，保证证明者P(x)的度是小于1000,000，Ψ(x)的度小于10,000,000-1000,000。这就是LDT的目标，那LDT具体的过程是怎么样的呢？请继续往下看。

举个栗子，如果Alice想证明多项式f(x)的度是小于3的，即有可能是2次的或者是1次的。一般流程如下：

验证者Bob随机选取三个值a,b,c，发送给证明者Alice；

证明者Alice返回f(a),f(b),f(c)；

验证者Bob插值出度小于3的多项式g(x)，然后再随机选取一个点d，发送给证明者；

声音 | 浙江大学区块链研究中心蔡亮：中国区块链技术发展的重点是自主可控的联盟链:据新华社消息，浙江大学区块链研究中心常务副主任蔡亮教授表示，西方区块链的技术发展重点是公有链，应用和产业发展重点是基于公有链的金融创新，而中国区块链技术发展的重点是自主可控的联盟链，应用和产业发展的重点是区块链如何服务于产业经济、政府服务和社会治理。多名专家和业内人士表示，区块链技术未来在我国政务、金融、民生等相关领域具有广阔应用前景。比如通过区块链技术，可以实现政务数据的分布式共享；再比如，供应链上的龙头企业可以通过区块链将自己的信用传导到小微企业，进而部分解决融资难、融资贵的问题。“如何解决联盟区块链的效率与安全问题，如何解决链上链下数据协同问题，如何解决区块链的监管问题，是未来发展的重要方向。”蔡亮表示，只有解决好上述问题，区块链才能真正服务好我们的经济社会发展。[2019/10/26]

证明者Alice返回f(d)；

验证者Bob比对f(d)和g(d)的值，如果相等，则证明成立。

回归到一般情况，其过程可以用下图3表示：

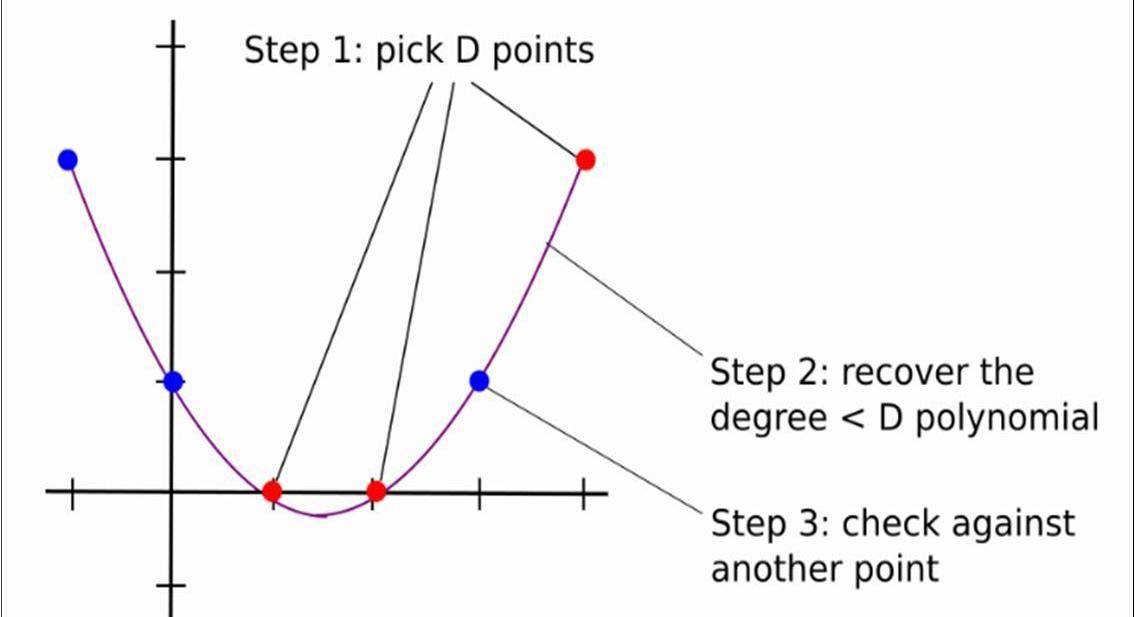
可以看出，如果D很大，Alice和Bob交互的次数则为D+k次，复杂度很高；有没有一种办法，使得两者之间交互的次数小于D的情况下，使得验证者相信多项式的度是小于D的，直接返回小于D个点肯定是不行的，因为那不能唯一确定一个度小于D的多项式，因此需要证明者需要额外发送一些辅助信息。下面我们以P(x)为例，详细阐述这个过程(事实上，应该是证明P(x)和Ψ(x)的线性组合小于10,000,000-1000,000，本文重点是LDT，因此只以P(x)为例，这并不影响对LDT的理解)。

动态 | 韩国行政安全部选用区块链等高新技术推进公共服务工作课题:据韩国中央日报消息，韩国行政安全部今日表示，今年选定了利用尖端信息技术促进公共服务事业的推进课题。该课题包括区块链、新技术基础电子商务交易出口专用通关系统、人工智能及大数据基础智能型咨询系统等，其目标是在年底之前构建完成服务部署。[2019/2/20]

假如P(x)=x+x^999+x^1001+x^999999=x+x^999+x*x^1000+x^999*(x^1000)^999;

此时，我们找到一个二维多项式G(x,y)，取值范围分别是、，满足：

G(x,y)=x+x^999+x*y+x^999*y^999可以发现，当y=x^1000时，满足：

G(x,y)=G(x,x^1000)=x+x^999+x*x^1000+x999*(x^1000)^999=P(x)

如果我们能证明G(x,y)相对的x,y的最高度都是小于1000，因为P(x)=G(x,x^1000)上，因此可以相信P(x)的度小于1000,000；如图4所示：

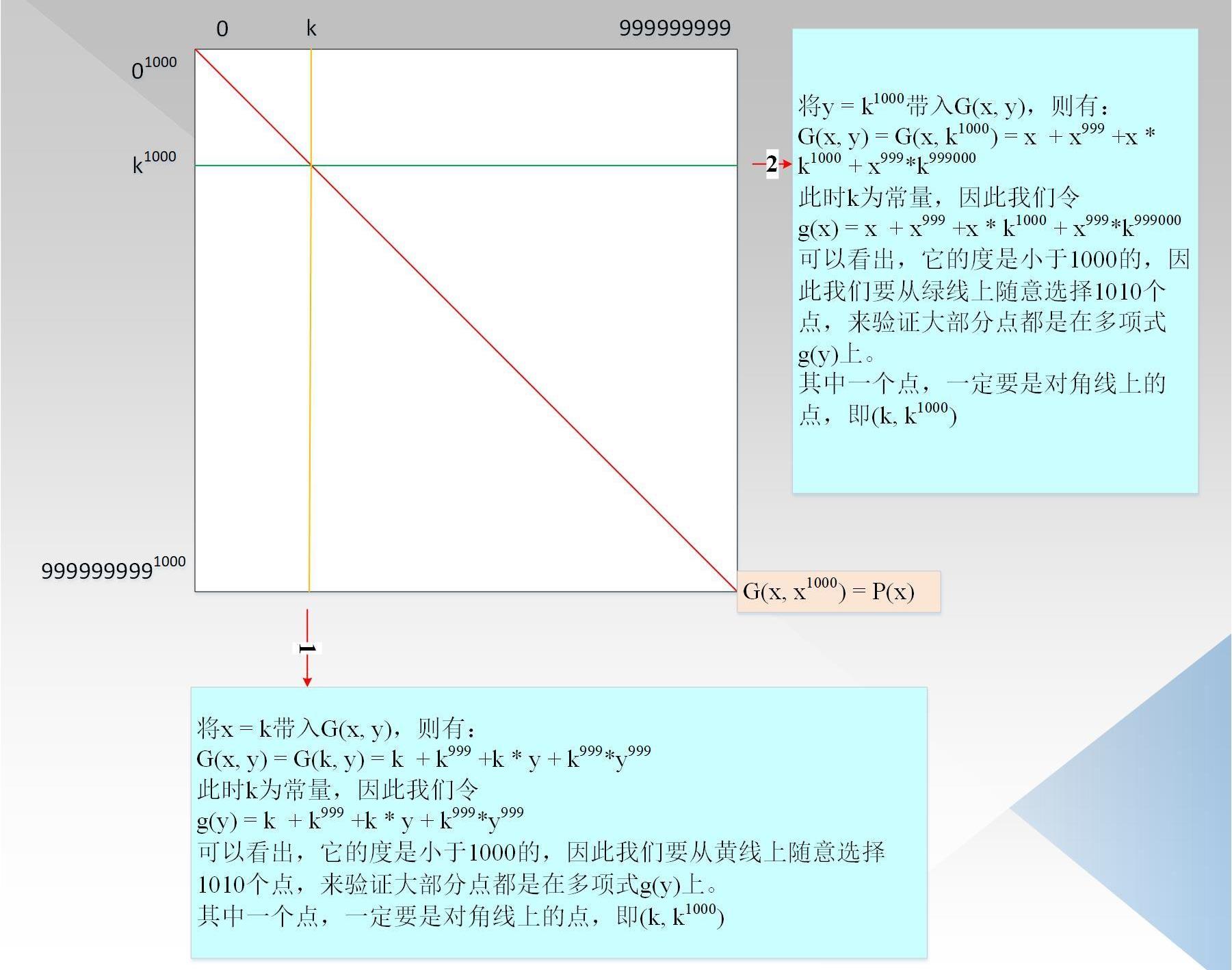
验证者把所有的点都计算好，形成一颗默克尔树。验证者随机选择一行和一列，如图中红线1/2所示，对于每一列，它是由关于y的度小于1000的多项式生成，对于每一行，它是由关于x的度小于1000的多项式生成。验证者从行/列中随机选择1010个点，用来验证对应行/列上的点是否在度小于1000的多项式上，需要注意的是，因为P(x)的点都在上图的对角线上，因此我们要确保每一行/列对应的对角线上的点也在对应的度小于1000的多项式上，即1010个里面一定要包含对角线的点。

甘肃省长：充分运用区块链等技术构建产业链条:6月12日上午，丝绸之路国际知识产权港建设工作第一次领导小组会议在兰州召开。省委副书记、省长唐仁健主持会议并讲话。唐仁健指出，在互联网、区块链等信息技术快速发展以及商业模式创新的背景下，甘肃作为丝绸之路经济带的重要节点、国家向西开放的重要门户和次区域合作战略基地，“一带一路”建设为建设国际知识产权港提供了重大历史机遇。要充分运用大数据、区块链等最前沿、最先进的现代信息技术手段，确保高起点谋划、高标准建设。要找准突破路径，坚持先易后难，分步推进，梳理明确今后1-3年的重点工作，逐步构建完善的知识产权服务体系和产业链条。[2018/6/13]

可靠性分析：如果原始多项式的度实际上是小于10^6+10999，即P(x)=x+x^999+x^1001+x^1010999，那么对应的G(x,y)为G(x,y)=x+x^999+x*y+x^999*y^1010，即，对于每一个x，G(x,y)是关于y的一元多项式函数，且度d<1010，因此下图中的每一列所有点都是在度d<1010的多项式上，而不在d<1000的多项式式上。所以如果证明者任然宣称多项式P(x)的度d<1000,000，则会验证失败，其他场景是同样的道理

那有没有可能恶意证明者仍以G(x,y)=x+x^999+x*y+x^999*y^999的形式去生成证据呢？这样会验证通过吗？

我们知道，我们在验证时着重强调了对角线上的那一点一定要在多项式上，我们知道，此时对角线对应的多项式形式是

P(x)=x+x^999+x1001+x^999999，而实际的P(x)，我们在这里标记为P`(x)，其形式是：

P`(x)=x+x^999+x^1001+x^1010999

因此，如果验证者恰好选择的点是两个多项式的交点，则会验证通过，事实上，两个多项式最多有1000,000左右个交点，但是由于随机选取的点不是证明者自己选取，是由默克尔树的根为种子随机生成，因此证明者没有机会作恶，去可以选取那些能通过验证的点。

由于总共由10^9个点，因此随机选取一个点，能验证成功的概率为10^6/10^9=10^(-3)，如果选择k行，则成功的概率仅为10^(-3k)。

以上可以看出，验证者和证明者只需要交互1010*2*k个点，就可以完成验证，假如k=10，则1010*2*10=20100<<10^6。

虽然上述实现了在交互次数小于D的情况下，完整LDT验证，但是证明者的复杂度过于庞大，至少10^18的复杂度远远大于原始的计算，因此需要一些优化方案，降低复杂度。话不多说，直接引入有限域，毕竟在实际项目中，我们可不希望数值本身过于庞大。直接引用费马小定理的结论：在有限域p内，如果满足(p-1)能被k整除，则映射x=>x^k的像只有(p-1)/k+1个。下图5以p=17，映射x=>x^2为例：

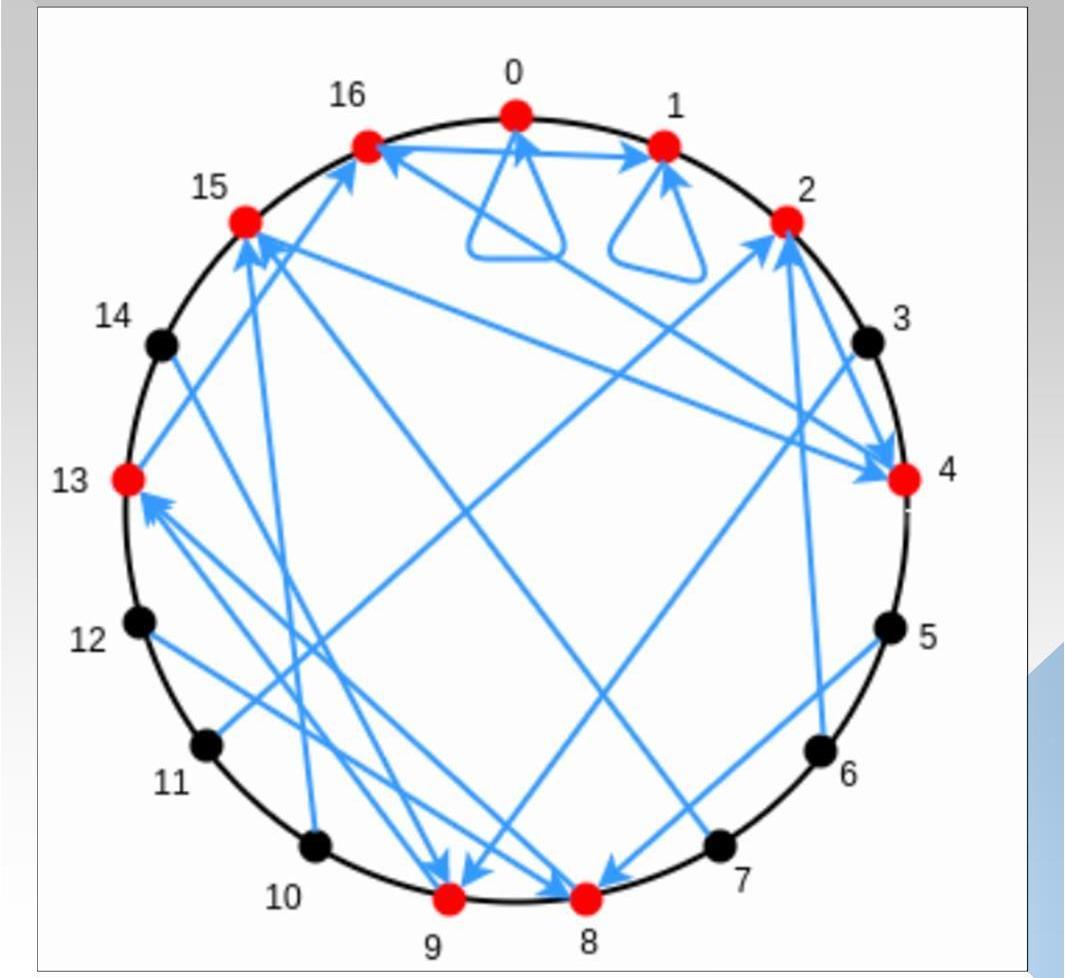
图中，红色为x^2在有限域p内的象，总共由(p-1)/2+1=9个。同时我们可以发现，9^2和8^2的像一致，10^2和7^2的像一致，以此类推，16^2和1^2的像一致，记住这个现象，对下一张图的理解有帮助。

因此，在本例中，我们选择一个素数p=1000,005,001，其满足：

为素数

p-1能被1000整除

p要大于10^9

因此，在有限域p内，x=>x^1000的像在p内有(p-1)/1000=1000,005个，因此图4可以变成图6的形式：

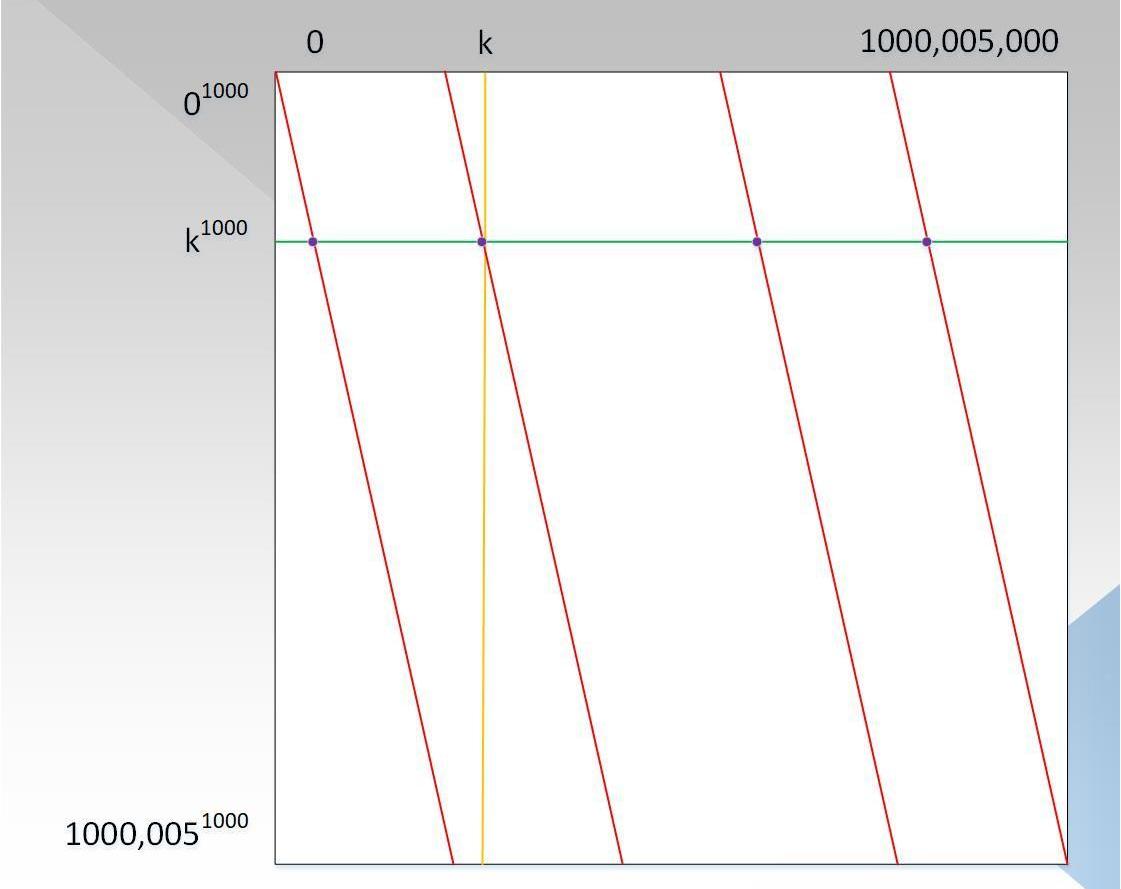
可以看出，列坐标变成了10^6个元素，对角线变成了平行的线条，总共有1000个。还记得上面费马小定理结论的特殊现象吗？这就是对角线这种分布的原因，读者试着去理解(可能读者会觉得，对角线应该是锯齿形，不是这种平行的形式，也许你是对的，但是这并不影响验证流程)。此时证明者的复杂度已经从10^18减少到了10^15次方，证明和验证过程和步骤3描述的仍然一致。

还能不能继续优化呢？答案是肯定的。回想起前面所述的验证过程，对于每一行/列，验证者都要获取1000个点进行插值得出一个度小于1000的多项式，仔细观察图6，对于每一行，原始数据里不就是有1000个数么？那我们干脆选这些点插值出一个度小于1000的多项式，然后只需要随机让证明者再计算任何一列，并且证明沿着列上的点都在度小于1000的多项式上，并且列上的点也在对应的利用原始数据插值出的行多项式上。此时，证明者复杂度从10^15减少到了10^9次方。

总结：个人理解，从步骤1到步骤5，其实是PCP到IOP的选择过程。

PCP要求证明者生成全部的证据，然后验证者多次随机选取其中的某一部分进行验证，但是这样，证明者的复杂度仍然很高；

IOP要求证明者不用生成全部的证据，根据多次的交互，每次生成只需生成部分证据，使得证明的复杂度和D呈近似线性关系；

证明者复杂度已经降低到了与D呈拟线性关系，验证者的复杂度虽然是亚线性，交互次数已经低于D，但是能不能优化到更低呢？基于证明复杂度的最优设置，我们继续探索验证复杂度的优化之路，回顾P(x)=x+x^999+x^1001+x^999999=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999，令G(x,y)=x+x*y^499+x*y^500+x*y^499999，则当y=x^2时，有G(x,y)=G(x,x^2)=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999=P(x)。最终的图应如下图7所示：

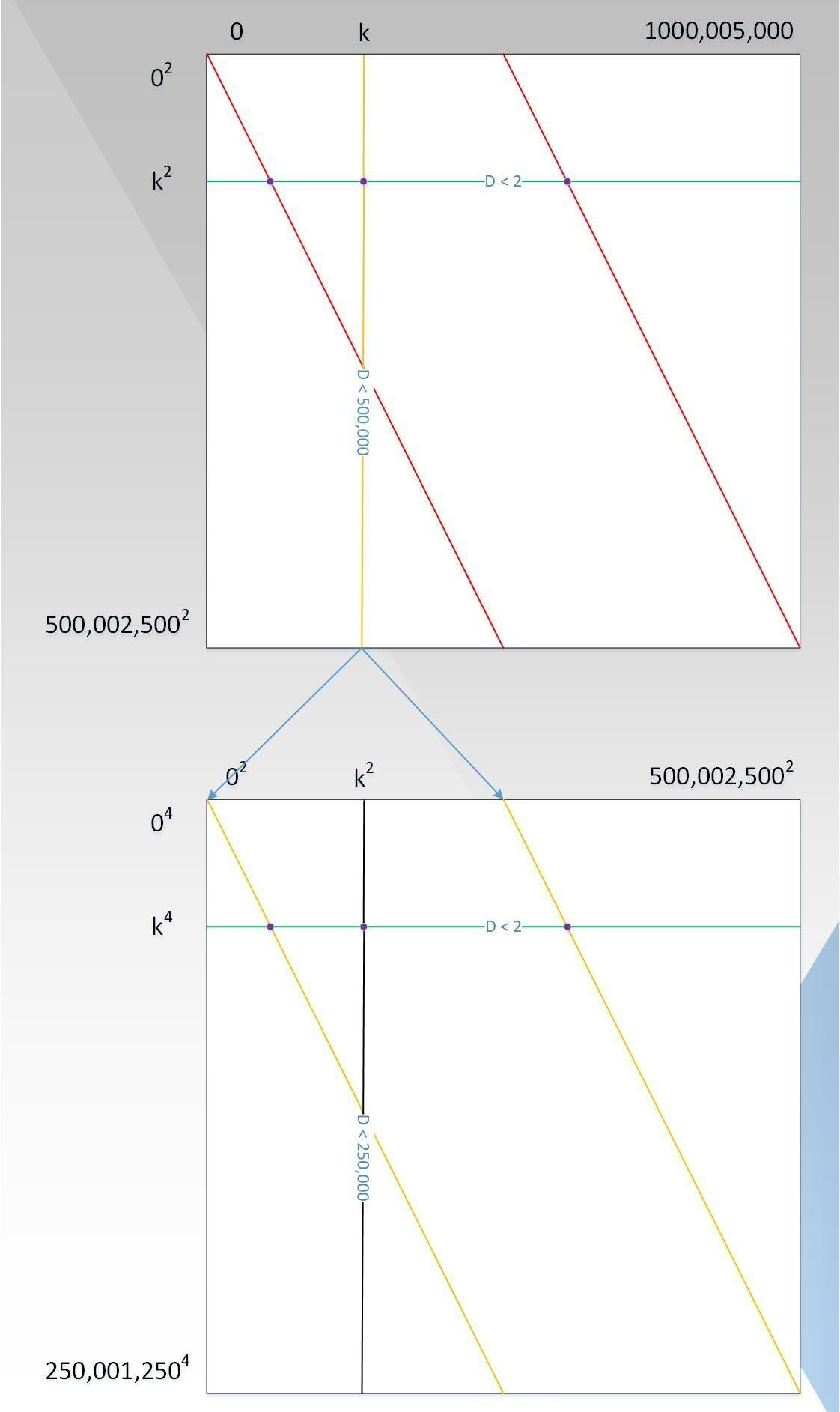
从图中可知：

证明则复杂度仍为10^9次方；

每一行上的点都在度d<2的多项式上，因为当y取固定值时，G(x,y)就是关于x的一次多项式；

每一列上的点都在度d<D/2的多项式上，证明者需要证明这个多项式是小于D/2的，假定这个多项式为P1(x)，这个时候，并非验证者选取大于D/2个点去验证，因为验证复杂度仍然不够低，而是对这一列再一次用到类似于P(x)的处理过程，如图7中下面的图所示，以此循环，直到可以直接判断列上的多项式的度为止，类似于行。

总结

至此，本篇文章就结束了，总结下来，本文主要阐述了以下几个内容：

如何转换问题形式--Arithmetization

为何需要LDT--为了验证简洁

LDT的大概过程--二分法验证，类似于FFT

降低LDT的复杂度--有限域+IOP

至于LDT的详细过程，将留给本系列的最后一篇，敬请关注。

谢谢大家，欢迎批评指正，有任何问题或者疑问可以留言。

标签：区块链LICICEALI区块链专业方向好就业吗alice币怎么样Giving To Services

SOL热门资讯