技术干货 | 理解零知识证明算法之Bulletproofs：Range Proof I

前言

Bulletproofs，又一个有意思的零知识证明算法，相信读者已经很熟悉它了。和zk-snark相比，它不需要可信设置；和zk-stark算法相比，它具有较小的proofsize。根据论文，它有两个方面的应用：1.用于rangeproof；2.用于一般算术电路的零知识证明。下面，让我们先看一下Bulletproofs是如何高效的实现第一点。

Rangeproof

1.?预备知识

aL：表示向量{a1,a2……an}

2n：表示向量{20,21…2n-1}

<a,b>：表示向量内积∑ai*bi，结果是一个值

aob：向量对应位相乘，{a1*b1……an*bn}，结果是一个向量

2.?证明

Alice想要证明

v?

=>则，需要证明一个relation得成立，如下所示：

{：V=grhv^v?}

public-x??????????witness-wrelation-R

即，对于公开信息x，Alice有隐私信息w，使得关系R成立。

令aL为金额v的在范围内的二进制形式，则aL={a1,a2……an}?{0,1}n，且满足<aL,2n>=v。因此，证明者需要证明以下几个等式相等：

香港金管局总裁：DeFi未来或成为金融领域创新的重要技术:7月18日消息，香港金融管理局总裁余伟文在G20金融官员会议上表示，对Stablecoin进行更严格的审查有助于防止DeFi领域的灾难，因为Stablecoin通常用于购买其他加密货币，然后用于去中心化金融活动。余伟文认为监管Stablecoin比监管DeFi、及其相关产品要好。

同时他也表示DeFi不会很快消失，并且可能会成为关注金融领域未来创新的重要技术。在私营Token监管方面，余伟文认为私营发行的Token需要得到监管，这对于解决去中心化金融带来的风险至关重要。（beincrypto）[2022/7/18 2:19:56]

V=grhv????(1)

<aL,2n>=v???(2)

aLoaR=0n??(3)

aR=aL-1n???(4)

等式(1)确保了承诺V和金额v的绑定关系，等式(2)确保了v的范围，等式(3)(4)确保了a

L元素只属于{0,1}。等式(2)/(3)/(4)总共包含了2n+1个约束，其中公式(2)1个，公式(3)(4)各n个。接下来，为了效率，我们需要把2n+1个约束转换成1个约束。

3.?2n+1个约束转换成1个约束

=>预备：从Zp中任意选择一个数y，则b=0n是等式<b,yn>=0成立的充分条件；因为当b!=0n，等式成立的概率仅有n/p，p是有限域，远大于n。因此，如果有<b,yn>=0，那么验证者愿意相信b!=0n。

报告：10%的早期初创企业专注于区块链技术:9月26日消息，一份新报告显示，10%的早期初创企业专注于这项技术。区块链与人工智能、大数据和机器人并列为增长最快的技术趋势。区块链是全球初创企业中增长最快的技术之一。

在过去的五年里，区块链经历快速采用，超越了数字货币和金融，成为社交媒体、医疗保健、供应链管理、大数据、法律服务、保险和许多其他行业的支柱。最新的《全球初创企业生态系统报告（Global Startup Ecosystem Report）》反映了这种采用率的上升，将区块链列为值得关注的行业之一，尤其是在早期初创企业中。该年度报告由政策咨询机构Startup Genome编制，调查了全球1万多名初创企业高管。（CoinGeek）[2021/9/27 17:09:10]

利用这个理论，我们把等式(2)/(3)/(4)做以下转换：

1.验证者随机选取一个数y发送给证明者；

2.证明者要证明：

<aL,2n>=v(5)

<aL,aRoyn>=0???????(6)

<aL-1n-aR,yn>=0???(7)

同理，等式(5)确保了v的范围，等式(6)(7)确保了a

L元素只属于{0,1}。此时2n+1个约束转换成3个约束，接下来，还需要做进一步的处理：

青岛“智能办”平台上线试运行，将区块链等技术与审批业务深度融合:5月7日，青岛“智能办”平台上线试运行，通过“青岛市行政审批微大厅”微信公众号同步新发30项“智能办”事项，其中28个涉企事项，包括社会团体印章备案、人力资源服务许可（延续）等12个业务领域。与“网上审批”“秒批”相比，“智能办”亮点更加突出。技术平台更加先进，建成全省首个、国内领先的综合性“智能办”平台。将大数据、人工智能、区块链等前沿技术与审批业务深度融合，在全省率先建成支撑市、区两级“智能审批”改革的综合性、一体化平台。（青岛日报）[2020/5/9]

1.验证者随机选取一个数z发送给证明者：

2.证明者利用z对公式(5)(6)(7)进行线性组合，得到如下公式：

z2*<aL,2n>+z*<aL-1n-aR,yn>+<aL,aRoyn>=z2*v???(8)

至此，我们已经把2n+1个约束转换成1个约束。下面我们对公式(8)做进一步的优化，把三个点积优化成1个点积

4.?三个点积优化成1个点积

=>z2*<aL,2n>+z*?<aL-1n-aR,yn>+<aL,aRoyn>=z2*v

=><aL,z2*2n>+<aL,z*yn>-<z*1n,yn>-<z*aR,yn>+<aL,aRoyn>=z2*v

动态 | 亚马逊在职位列表中修改广告金融技术团队的专注方向，取消对区块链技术的引用:此前，亚马逊在招募一名高级软件工程师加入“专注于区块链分布式账本的广告金融技术团队”，希望将其部分广告业务与区块链技术整合。但近期，亚马逊在职位列表中悄然取消了对区块链技术的引用，该广告团队专注于财务分类账、计费和对账系统，以提供跨国金融数据的数据透明度。（dailyhodl）[2019/8/9]

=><aL,aRoyn+z*yn+z2*2n>-<z*1n,yn>+<z*1n,ynoaR>=z2*v

=><aL,aRoyn+z*1noyn+z2*2n>-<z*1n,yn+ynoaR>=z2*v

=><aL,(aR+z*1n)oyn+z2*2n>-?<z*1n,yn+ynoaR>=z2*v

=><aL,(aR+z*1n)oyn+z2*2n>-?<z*1n,(aR+z*1n)oyn+z2*2n-z*1n*yn+yn-z2*2n>?=?z2*v

=>?<aL-z*1n,(aR+z*1n)oyn+z2*2n>-<z*1n,-z*1n*yn+yn-z2*2n>=?z2*v

=>?<aL-z*1n,(aR+z*1n)oyn+z2*2n>=z2*v+<z*1n,-z*1n*yn+yn-z2*2n>

Tradeshift利用区块链技术创建兼容的支付系统:据btcmanager消息，Tradeshift最近推出了一项名为Tradeshift Pay的服务，允许支付和财务解决方案与包括以太坊和hyperledger在内的所有主要区块链技术一起工作。该可互操作的解决方案可将所有交易写入公共总账，以确保明确记录并创造更大的透明度。Tradeshift Pay作为一个云平台，将供应链支付，供应链融资和基于区块链的早期支付整合到一个端到端的解决方案中。[2018/5/24]

=>?<aL-z*1n,(aR+z*1n)oyn+z2*2n>=z2*v+<z*1n,(-z*1n+1n)*yn>-<z*1n,?z2*2n>

=>?<aL-z*1n,(aR+z*1n)oyn+z2*2n>=z2*v+(z–z2)*<1n,yn>-z3*<1n,2n>???(9)

=>?令

L=?aL-z*1n

R=?(aR+z*1n)oyn+z2*2n

δ=?(z–z2)*<1n,yn>-z3*<1n,2n>

5.验证：

1.证明者把L/R/V发送给验证者；

2.验证者事先算好δ

3.验证者根据L算出来aL，根据<aL,2n>=v算出v

4.验证者根据L,R,v,δ验证等式<L,R>=z2*v+δ

因为y，z都是验证者提供，因此如果验证者如果能验证公式(9)成立，则相信等式(5)(6)(7)成立，则相信等式(2)(3)(4)成立，则相信v满足关系v?。

但是，可以看到上述过程，泄露了v的信息，因此需要一个零知识证明协议。

6.?一个零知识证明协议

由于L,R包含了v的相关信息，因此，我们需要添加两个盲因子s

L

、s

R来隐藏a

L，a

R。如公式(10)(11)所示：

l(X)=(aL-z*1n)+sL*X)??(10)

r(X)=(aR+z*1n+sR*X)oyn+z2*2n???(11)

此时，定义公式(12)

t(X)=<l(X),r(X)>=t0+t1*X+t2*X2???(12)

可以看出系数t

0是l(x)和r(x)常数项的乘积，即满足：

t0=<L,R>=z2*v+δ

因此，问题由证明：

<L,R>=z2*v+δ

转化成了，在任意一点x，验证者验证多项式值l(x),r(x),t(x)满足关系：

<l(x),r(x)>=t(x)

多项式值l(x),r(x),t(x)由证明者提供，为了保证l(x)，r(x)well-formed，即：

l(x)=(aL-z*1n)+sL*x)

r(x)=(aR+z*1n+sR*x)oyn+z2*2n

需要校验：

P=A*Sx*g(-z)*(h`)z*yn+z^2*2^n

=hαgaLhaR*(hρgsLhsR)x*g(-z)*(h`)z*y^n+z^2*2^n

=hαgaLhaR*?hρxgsL*xhsR*x*g(-z)*(h`)z*y^n+z^2*2^n

=hα+ρx*gaL+sL*x–z*1^n*haR+sR*x*(h`)z*y^n+z^2*2^n

=hα+ρx*gaL+sL*x–z*1^n*(h`)y^no(aR+sR*x)*(h`)z*y^n+z^2*2^n

=hα+ρx*gaL+sL*x–z*1^n*(h`)y^no(aR+sR*x)+z*y^n+z^2*2^n

=hα+ρx*gaL+sL*x–z*1^n*(h`)y^no(aR+sR*x+z*1^n)+z^2*2^n

=?hμgl(h`)r

=>当且仅当l/rwell-formed，等式成立

为了保证t(x)well-fromed，即：

t=t0+t1x+t2x2

需要校验：

=>gthτx=?Vz^2*gδ*T1x*T2x^2

=>gthτx=?(hrgv)z^2*gδ*(gt1)x*(hτ1)x*(gt2)x^2*(hτ2)x^2

=>gthτx=?hz^2*r+τ1*x+τ2*x^2*gz^2*v+δ+t1*x+t2*x^2

=>gthτx=?hz^2*r+τ1*x+τ2*x^2*gt0+t1*x+t2*x^2

=>t=?t0+t1*x+t2*x2&&τx=?z2*r+τ1*x+τ2*x2

=>当且仅当t和τxwelle-formed，等式成立

具体的协议流程图如下图所示：

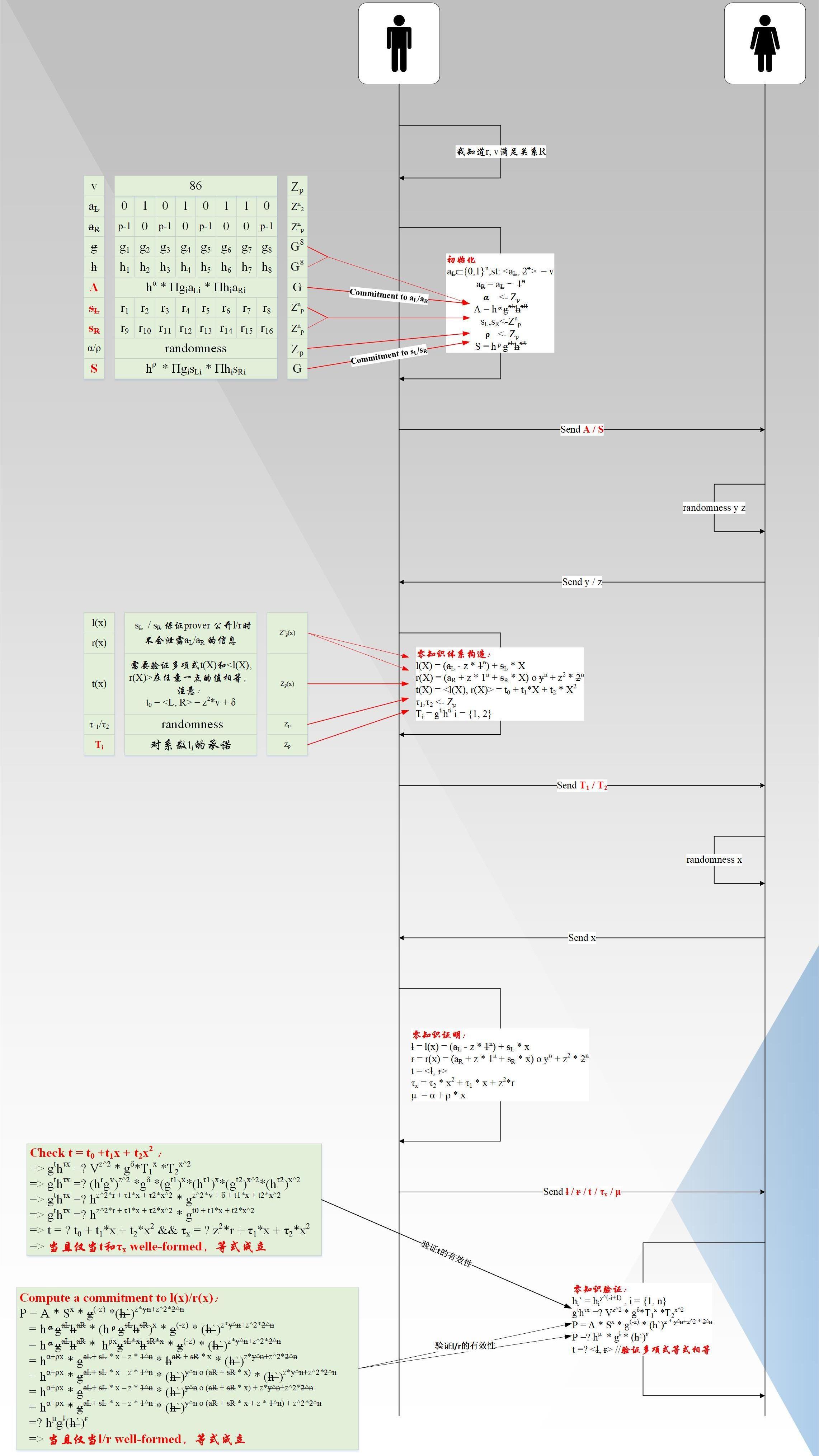
总结

从上述流程可以看出，一次rangeproof，证明者需要发送总共{

l/r/t/

τ

x

/

μ

/T1/T2/A/S}个元素给验证者，总共2n+3个Z

p元素，4个G元素。下一篇文章将细讲，Bulletproofs如何将交互复杂度降低到对数级O(log(n))

附录

1.Bulletproofs论文：

chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Feprint.iacr.org%2F2017%2F1066.pdf

标签：区块链ROOPROProof区块链技术运行在一个完全p2p的网络里Hamster GroomersPrometheus TradingRugProof

欧易okex官网热门资讯