深入理解零知识证明算法之Zk-stark：Low Degree Testing

前言

本系列的第二篇文章，以超市收据为例，描述了Arithmetization的具体过程。本文将以另外一个例子为基础，在回顾Arithmetization过程的同时，将内容引申到多项式的LDT过程。

新的实例

AliceClaim：“我有1000,000个数，他们都在范围内”。为了方便验证者Bob验证，Alice首先要对Claim进行Arithmetization转换。过程如下图1所示(图中：黑色箭头代表主流程，红色箭头代表附加说明信息，黄色圈对应下面详细说明的索引)

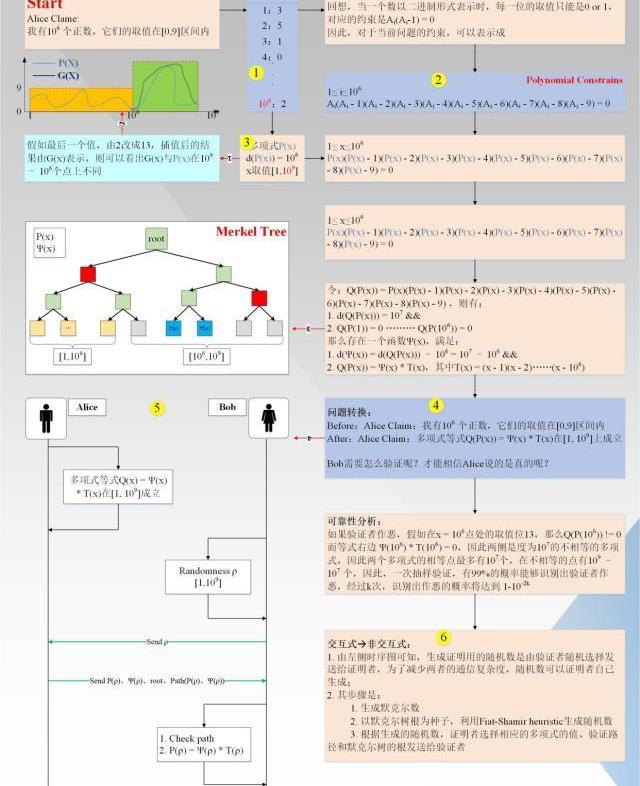
下面具体说明一下对应流程：

首先生成执行轨迹(EXCUTETRACE)，事实上，它是一张表，总共有1000,000行；生成多项式约束(PolynomialConstrains)，多项式约束满足执行轨迹的每一行(个人理解：步骤1，2没有一定的先后依赖关系，只是习惯上先生成执行轨迹，再生成约束多项式)；对执行轨迹进行插值，得到一个度小于1000,000的多项式P(x)、x取值，并计算更多点上的值，x取值范围扩大到(Reed-Solomen系统编码)；假如，证明者有一个值不在范围内(图中红线1/2所示)，假如就是第1000,000个点，它实际的值是13，大于9，其插值后的曲线G(x)如图所示，图中P(x)为有效曲线，G(x)为无效曲线。可以看出，两条曲线在变量x取值范围内，最多有1000,000个交点，即有1000,000,000-1000,000个点不同，这很重要。将插值后的多项式P(x)和多项式约束进行组合变换，最终得到的形式为：

Bondly获OKEx Blockdream Ventrues投资 双方将深入探索NFT领域:据官方消息，Bondly已获OKEx Blockdream Ventrues（OKEx BDV）投资，双方将深入探索NFT领域，为NFT优质区块链项目发展提供服务和资源支持。一方面，Bondly将通过NFT形式为OKEx BDV合作的优质项目提供LaunchPad服务；另一方面，双方共同把优秀品牌带到Bprotect，也将以NFT创新形式与OKExChain生态资产进行品牌合作。

Bondly是一种可互操作、透明、便捷的资产兑换协议，旨在彻底改变传统的资产托管方法，并使每个艺术创作人都能进入自己的数字市场，旗下产品包括BSwap（NFT发售平台）、Bondly LaunchPad（IDO平台）、BProtect（NFT交易平台)。OKEx BDV初始资金1 亿美金，致力于发现和投资最前沿的产品技术创新类区块链项目，投资方向包括基础设施、交易及金融项目、公链生态类项目、应用类流量入口等。[2021/5/6 21:28:39]

Q(P(x))=Ψ(x)*T(x)，其中T(x)=(x-1)(x-2)……(x-1000,000)，x取值

其中，d(Q(P(x)))=10,000,000、d(Ψ(x))=10,000,000-1000,000、d(T(x))=1000,000；

至此，问题就转化成了，Alice宣称“多项式等式在变量x取值范围内成立”的问题。那么验证者Bob该如何验证呢？具体过程如下：证明者Alice在本地计算多项式P(x)、Ψ(x)在所有点上的取值，对！从1至1000,000,000，并形成一个默克尔树；验证者Bob随机的从内选取一个值ρ，并发送给证明者Alice，要求其返回对应的信息；证明者Alice返回P(ρ)、Ψ(ρ)、root、AuthorizedPath(P(ρ)、Ψ(ρ))给验证者Bob；验证者Bob首先根据默克尔树验证路径验证值P(ρ)、Ψ(ρ)的有效性，然后等式Q(P(ρ))=Ψ(ρ)*T(ρ)，如果成立，则验证通过；

山西深入推进跨境金融区块链服务平台应用:国家外汇管理局山西省分局深入推进跨境金融区块链服务平台应用，为中小微外贸企业跨境结算与融资扩渠道、增便利。目前，山西省已有17家银行加入该平台，为16家企业办理融资业务116笔，累计放款7.67亿美元。（中国新闻网）[2020/5/3]

完整性分析：如果验证者Alice是诚实的，那么等式Q(P(x))一定会被目标多项式T(x)整除，因此必定存在一个d(Ψ(x))=d(Q(P(x)))-d(T(x))的多项式Ψ(x)，满足Q(P(x))=Ψ(x)*T(x)，因此对于任意的x，取值在之间，等式都会成立；

可靠性分析：如果验证者Alice是不诚实的，即类似于步骤3里的假设，在x=1000,000上，P(x)的取值为13，那么Q(P(1000,000))!=0，但是等式右边，T(1000,000)=0，因此Q(P(x))!=Ψ(x)*T(x)，即等式两边是不相等的多项式，其交点最多有10,000,000个，因此通过一次随机选取，其验证通过的概率仅为10,000,000/1000,000,000=1/100=0.01，经过k次验证，其验证通过的概率仅是1-10(^-2k)；

上述的验证过程为交互式的，如果是非交互式的，可以利用Fiat-Shamirheuristic进行变换，以默克尔树的根作为随机源，生成要查询的随机点；

LDT

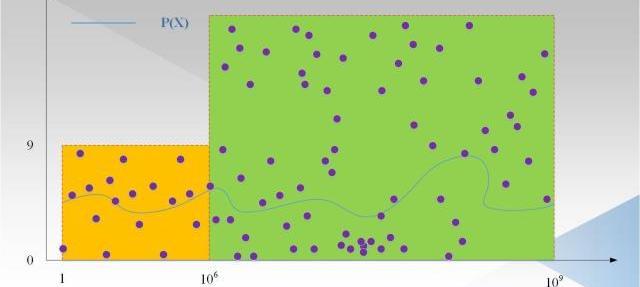
我们忽略了一种攻击方式，即针对每一个数x，证明者都随机生成p，然后根据Ψ(x)=Q(p)/T(x)，这些点不在任何一个度小于1000,000的多项式上，但是可以通过验证者验证。如下图2所示：

动态 | 重庆两江新区与重庆市科学技术研究院达成合作 双方将在区块链等领域深入探讨合作:金色财经报道，重庆两江新区与重庆市科学技术研究院27日在当地签署全面战略合作协议。双方要在区块链等领域深入探讨合作。[2019/11/28]

图中：紫色的点为随机生成的点p，这些点大概率不在一个度小于1000,000的多项式上(事实上，可以不考虑前1000,000个点，因为验证者只会从范围内取值)。因为即使选择1000,000个点插值出一个度小于1000,000的多项式，也不能保证其他的点在这个多项式上，因为其他的点是随机生成的。因此，需要有一种方式，保证证明者P(x)的度是小于1000,000，Ψ(x)的度小于10,000,000-1000,000。这就是LDT的目标，那LDT具体的过程是怎么样的呢？请继续往下看。

举个栗子，如果Alice想证明多项式f(x)的度是小于3的，即有可能是2次的或者是1次的。一般流程如下：

验证者Bob随机选取三个值a,b,c，发送给证明者Alice；证明者Alice返回f(a),f(b),f(c)；验证者Bob插值出度小于3的多项式g(x)，然后再随机选取一个点d，发送给证明者；证明者Alice返回f(d)；验证者Bob比对f(d)和g(d)的值，如果相等，则证明成立。

回归到一般情况，其过程可以用下图3表示：

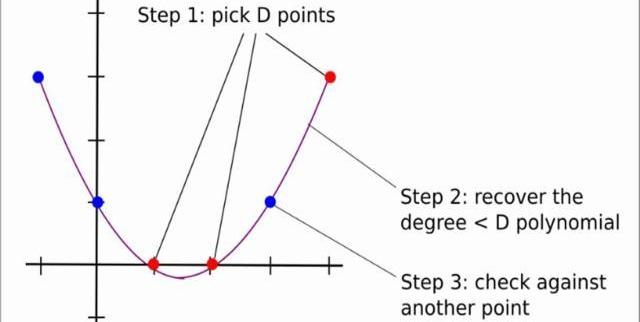
可以看出，如果D很大，Alice和Bob交互的次数则为D+k次，复杂度很高；有没有一种办法，使得两者之间交互的次数小于D的情况下，使得验证者相信多项式的度是小于D的，直接返回小于D个点肯定是不行的，因为那不能唯一确定一个度小于D的多项式，因此需要证明者需要额外发送一些辅助信息。下面我们以P(x)为例，详细阐述这个过程(事实上，应该是证明P(x)和Ψ(x)的线性组合小于10,000,000-1000,000，本文重点是LDT，因此只以P(x)为例，这并不影响对LDT的理解)。

声音 | 中国互金协会副秘书长：我国区块链在金融领域应用总体处于早期尝试向深入探索转变的过渡阶段:金色财经报道，11月20日，“金融进化论：2019新京报金融科技论坛”上，中国互金协会副秘书长杨农表示，当前，我国区块链在金融领域应用，已在供应链金融、金融数据共享和金融信息存证等场景中形成了一些落地案例，总体处于早期尝试向深入探索转变的过渡阶段，且呈现出探索性应用数量较多、参与主体较为多元、底层技术原创有待加强等特点。同时，区块链在我国金融领域的应用探索也面临着如下几个方面的挑战：技术层面仍难以兼顾部分金融应用场景对安全、功能和性能的要求；研发层面自主创新有待加强，对国外开源程序的广泛应用可能导致技术依赖风险；业务层面部分金融应用环节尚存在模糊地带，部分机构在开展区块链应用创新时缺少权威的第三方评估意见作为参考；治理层面存在法律规制困难，如链上资产和智能合约等方面的法律有效性界定不清晰。[2019/11/22]

假如P(x)=x+x^999+x^1001+x^999999=x+x^999+x*x^1000+x^999*(x^1000)^999;此时，我们找到一个二维多项式G(x,y)，取值范围分别是、，满足：G(x,y)=x+x^999+x*y+x^999*y^999可以发现，当y=x^1000时，满足：G(x,y)=G(x,x^1000)=x+x^999+x*x^1000+x999*(x^1000)^999=P(x)如果我们能证明G(x,y)相对的x,y的最高度都是小于1000，因为P(x)=G(x,x^1000)上，因此可以相信P(x)的度小于1000,000；如图4所示：

贵阳高新区党工委副书记黄昌祥：深入推进区块链等技术与实体经济深度融合:贵阳网6月4日报道， 日前，高新区党工委副书记、管委会主任黄昌祥率队对区内大数据创新平台进行调研。黄昌祥要求，大力实施“千企引进”“万企融合”“千企改造”等工程，推进“智力收割机”计划，深入推进物联网、人工智能、区块链以及大数据与实体经济深度融合，引领大数据技术创新、加快大数据产业聚集，构筑大数据产业生态体系，以大数据引领全区经济实现高质量发展。[2018/6/4]

验证者把所有的点都计算好，形成一颗默克尔树。验证者随机选择一行和一列，如图中红线1/2所示，对于每一列，它是由关于y的度小于1000的多项式生成，对于每一行，它是由关于x的度小于1000的多项式生成。验证者从行/列中随机选择1010个点，用来验证对应行/列上的点是否在度小于1000的多项式上，需要注意的是，因为P(x)的点都在上图的对角线上，因此我们要确保每一行/列对应的对角线上的点也在对应的度小于1000的多项式上，即1010个里面一定要包含对角线的点。

可靠性分析：如果原始多项式的度实际上是小于10^6+10999，即P(x)=x+x^999+x^1001+x^1010999，那么对应的G(x,y)为G(x,y)=x+x^999+x*y+x^999*y^1010，即，对于每一个x，G(x,y)是关于y的一元多项式函数，且度d<1010，因此下图中的每一列所有点都是在度d<1010的多项式上，而不在d<1000的多项式式上。所以如果证明者任然宣称多项式P(x)的度d<1000,000，则会验证失败，其他场景是同样的道理

那有没有可能恶意证明者仍以G(x,y)=x+x^999+x*y+x^999*y^999的形式去生成证据呢？这样会验证通过吗？

我们知道，我们在验证时着重强调了对角线上的那一点一定要在多项式上，我们知道，此时对角线对应的多项式形式是

P(x)=x+x^999+x1001+x^999999，而实际的P(x)，我们在这里标记为P`(x)，其形式是：

P`(x)=x+x^999+x^1001+x^1010999

因此，如果验证者恰好选择的点是两个多项式的交点，则会验证通过，事实上，两个多项式最多有1000,000左右个交点，但是由于随机选取的点不是证明者自己选取，是由默克尔树的根为种子随机生成，因此证明者没有机会作恶，去可以选取那些能通过验证的点。

由于总共由10^9个点，因此随机选取一个点，能验证成功的概率为10^6/10^9=10^(-3)，如果选择k行，则成功的概率仅为10^(-3k)。

以上可以看出，验证者和证明者只需要交互1010*2*k个点，就可以完成验证，假如k=10，则1010*2*10=20100<<10^6。

虽然上述实现了在交互次数小于D的情况下，完整LDT验证，但是证明者的复杂度过于庞大，至少10^18的复杂度远远大于原始的计算，因此需要一些优化方案，降低复杂度。话不多说，直接引入有限域，毕竟在实际项目中，我们可不希望数值本身过于庞大。直接引用费马小定理的结论：在有限域p内，如果满足(p-1)能被k整除，则映射x=>x^k的像只有(p-1)/k+1个。下图5以p=17，映射x=>x^2为例：

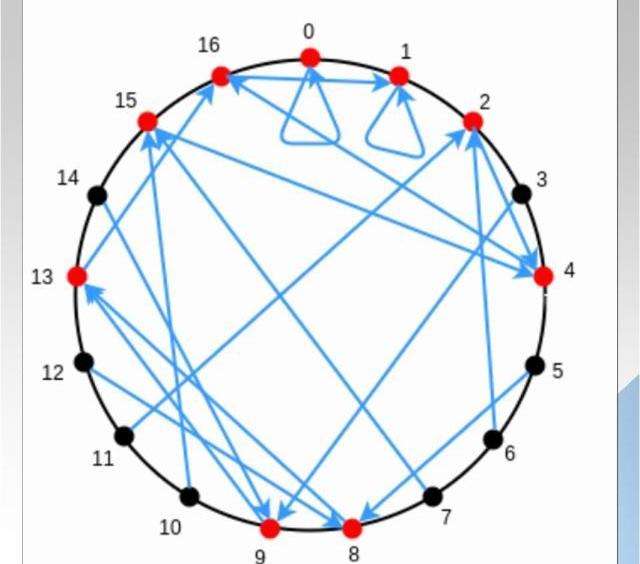
图中，红色为x^2在有限域p内的象，总共由(p-1)/2+1=9个。同时我们可以发现，9^2和8^2的像一致，10^2和7^2的像一致，以此类推，16^2和1^2的像一致，记住这个现象，对下一张图的理解有帮助。

因此，在本例中，我们选择一个素数p=1000,005,001，其满足：

为素数p-1能被1000整除p要大于10^9

因此，在有限域p内，x=>x^1000的像在p内有(p-1)/1000=1000,005个，因此图4可以变成图6的形式：

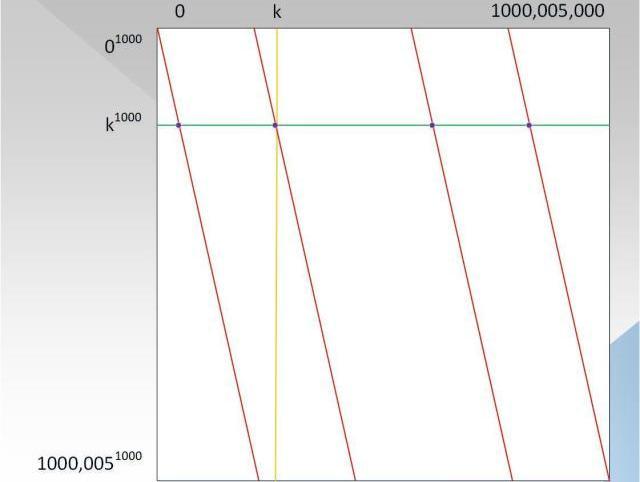
可以看出，列坐标变成了10^6个元素，对角线变成了平行的线条，总共有1000个。还记得上面费马小定理结论的特殊现象吗？这就是对角线这种分布的原因，读者试着去理解(可能读者会觉得，对角线应该是锯齿形，不是这种平行的形式，也许你是对的，但是这并不影响验证流程)。此时证明者的复杂度已经从10^18减少到了10^15次方，证明和验证过程和步骤3描述的仍然一致。

还能不能继续优化呢？答案是肯定的。回想起前面所述的验证过程，对于每一行/列，验证者都要获取1000个点进行插值得出一个度小于1000的多项式，仔细观察图6，对于每一行，原始数据里不就是有1000个数么？那我们干脆选这些点插值出一个度小于1000的多项式，然后只需要随机让证明者再计算任何一列，并且证明沿着列上的点都在度小于1000的多项式上，并且列上的点也在对应的利用原始数据插值出的行多项式上。此时，证明者复杂度从10^15减少到了10^9次方。总结：个人理解，从步骤1到步骤5，其实是PCP到IOP的选择过程。PCP要求证明者生成全部的证据，然后验证者多次随机选取其中的某一部分进行验证，但是这样，证明者的复杂度仍然很高；IOP要求证明者不用生成全部的证据，根据多次的交互，每次生成只需生成部分证据，使得证明的复杂度和D呈近似线性关系；证明者复杂度已经降低到了与D呈拟线性关系，验证者的复杂度虽然是亚线性，交互次数已经低于D，但是能不能优化到更低呢？基于证明复杂度的最优设置，我们继续探索验证复杂度的优化之路，回顾P(x)=x+x^999+x^1001+x^999999=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999，令G(x,y)=x+x*y^499+x*y^500+x*y^499999，则当y=x^2时，有G(x,y)=G(x,x^2)=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999=P(x)。最终的图应如下图7所示：

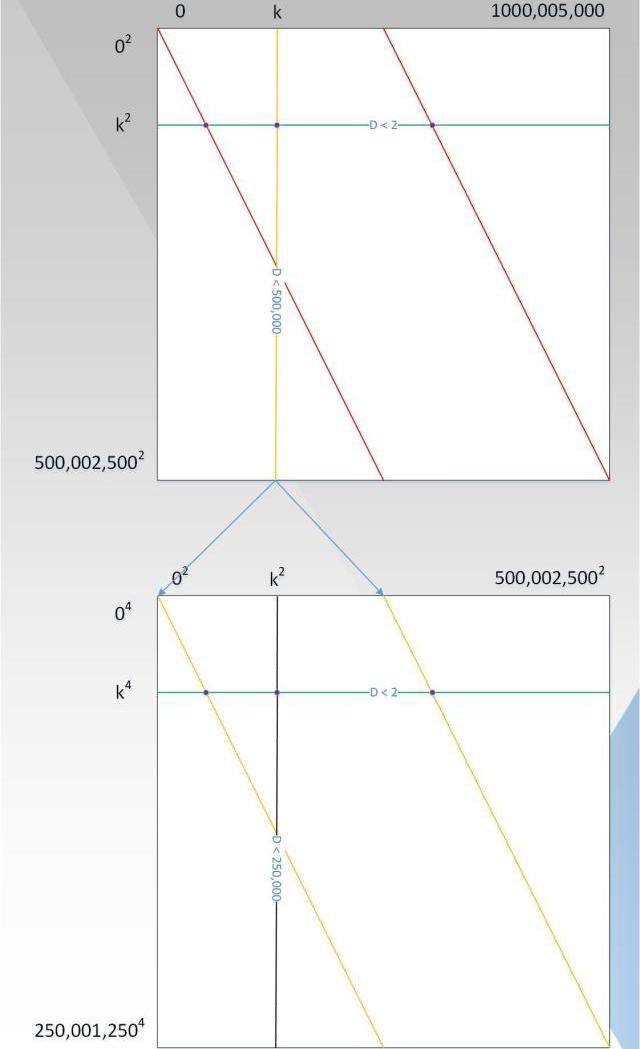
从图中可知：

证明则复杂度仍为10^9次方；每一行上的点都在度d<2的多项式上，因为当y取固定值时，G(x,y)就是关于x的一次多项式；每一列上的点都在度d<D/2的多项式上，证明者需要证明这个多项式是小于D/2的，假定这个多项式为P1(x)，这个时候，并非验证者选取大于D/2个点去验证，因为验证复杂度仍然不够低，而是对这一列再一次用到类似于P(x)的处理过程，如图7中下面的图所示，以此循环，直到可以直接判断列上的多项式的度为止，类似于行。

总结

至此，本篇文章就结束了，总结下来，本文主要阐述了以下几个内容：

如何转换问题形式--Arithmetization为何需要LDT--为了验证简洁LDT的大概过程--二分法验证，类似于FFT降低LDT的复杂度--有限域+IOP

标签：LDTIOPTRACLDT币LDT价格IOP币IOP价格TRAC币TRAC价格

酷币下载热门资讯