零知识证明： Plookup算法介绍

最近有空看了看Plookup的论文。针对对电路描述不友好的操作（比如bit操作），Plookup给出了新的思路和证明方式。给定某个操作的真值表示（lookup table），证明某个操作的输入/输出是在真值表中。这种方式，相对之前的bit计算约束方式，降低约束的个数，提高了电路效率。

Plookup的论文下载地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup尝试解决的问题是，给定两个集合，证明某个集合的元素在另外一个集合中。给定两个集合t和f，s是f排序后的结果。如果t中的元素最少在f中出现过一次。判别f中的元素是否包括在t中，只需要比较元素差的集合：

加密卫星公司Cryptosat和DoraHacks在国际空间站完成零知识证明实验:1月12日消息，加密卫星开发商 Cryptosat 和全球黑客马拉松组织者 DoraHacks 合作，在国际空间站 (ISS) 上进行了第一个在太空中发射零知识 (ZK) 证明系统的成功实验。DoraHacks 和 Cryptosat 表示，在国际空间站上进行的实验证明了基于卫星的计算环境能够执行使用 ZK 证明协议所需的部分可信设置过程。 Cryptosat 称，ZK 证明实验的成功是证明空间计算环境有效性的重要一步，Cryptosat 正在寻求将一组立方体卫星送入轨道并建立其卫星群。[2023/1/13 11:09:04]

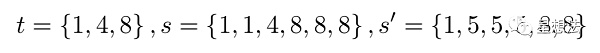
动态 | 波场社区TRONZ团队已完成零知识证明匿名交易公测:波场社区TRONZ团队已完成零知识证明匿名交易公测，测试网已经顺利部署。匿名交易即将在波场TRON主网上线，现已开启主网MPC流程，社区用户均可参与。Github参考地址可见原文链接。[2019/12/31]

举个例子，t是{1，4，8}的集合，元素的差异集合为{3, 4}，分别是4-1，8-4。如果s只有t中的元素组成，并且每个元素最少出现一次，例如{1，1，4，8，8，8}，元素的差异集合也为{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差异集合一样的情况下，也不能说明s中元素在t的集合中。例如s为{1，5，5，5，8，8}，元素的差异集合也为{3，4}，分别是8-5，5-1。

声音 | V神：零知识证明技术对Layer 2更有帮助:在万向区块链实验室主办的第五届区块链全球峰会上，当被问及最新进展时，V神表示目前正在关注零知识证明，该技术经过十几年的发展仍然有创新，Zk-SNARKs就取得了一些进步。V神还表示，零知识证明对Layer 2 也许并没有太大帮助，但对Layer 2也许会有帮助。[2019/9/18]

论文提出，可以引入一个随机因子，将前后两个元素相加的方法，确定两个集合的依赖关系。

定义多项式

在基本思想的基础上，论文在第三章定义了两个多项式F和G：

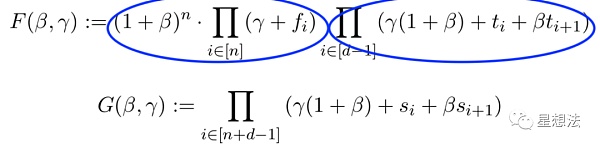
如果F和G相互对等，有且如下的条件成立：

f集合属于t

s是(f，t)的并集，并且按照t中的元素排序

如果条件成立，可以推导出两个多项式相等。F多项式可以看成是两部分组成，分别是两个连乘。后面的连乘可以看成是t中的元素连乘。前面的连乘，可以看成是f中元素的连乘。因为f中的元素属于t，则f中的元素的连乘，可以想象成多个相同元素的连乘。反之，因为beta和gamma的随机因子，也能从F和G对等条件推出满足的两个条件。具体的证明过程，可以查看论文的第三章。

在定义多项式的基础上，问题可以转化成两个多项式相等。

Plookup协议

已知f和t，可以排序得到s。因为s由f和t合并而成，s可以由两个函数h1和h2表示。关键在于第4步，定义了Z函数：

Z(g) = 1 - 初始为1

Z(x) 是两种多项式表示的商

Z(g^(n+1)) = 1 - n+1元素的连乘，两种多项式表达式相等

验证者，除了查看Z函数外，额外还要查看h1/h2连续性。

论文进一步将协议推广到更通用的情况，并给出了t中元素是连续情况下的优化协议。感兴趣的小伙伴可以自行查看。

Plookup提出了一种明确输入/输出的情况下，如何证明某个函数的运算正确的协议。输入输出定义成lookup表，计算的输入/结果只要在该lookup表中即表示运算正确。和Plonk采用同样的思路，Plookup定义了问题的多项式表示，证明了Z函数的递归表示和边界。

标签：OKULOOKPLOSATSOKUlooks币前景怎么样Employment CoinSATS币

DOGE热门资讯