一文读懂Schnorr签名如何提升比特币

在阅读Blockstream撰写的MuSig论文时，我一直在想象，这对于我一个比特币用户来说，到底意味着什么。我发现Schnorr签名的一些特性实在是非常棒而且便利，但某一些特性则非常烦人。在这篇文章里，我希望能跟各位分享我的想法。不过，我们先快速回顾一下。椭圆曲线签名算法

当前比特币的所有权体系用的是ECDSA。在签名一条消息m时，我们先哈希这条消息，得出一个哈希值，即z=hash(m)。我们也需要一个随机数k。在这里，我们不希望信任随机数生成器，所以我们通常使用RFC6979，基于我们所知的一个秘密值和我们要签名的消息，计算出一个确定性的k。使用私钥pk，我们可以为消息m生成一个签名，签名由两个数组成：r和s=(z+r*pk)/k。然后，使用我们的公钥P=pk*G，任何人都可以验证我们的签名，也就是检查(z/s)×G+(r/s)×P的x坐标确为r。

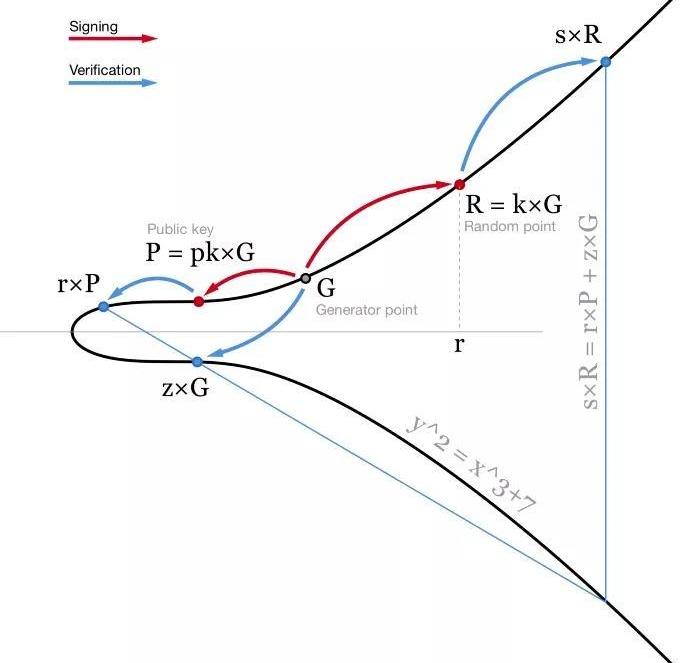
-ECDSA算法图解。为便于说明，椭圆曲线作在实数域上-这种算法是很常见的，也非常好用。但还有提升空间。首先，签名的验证包含除法和两次点乘法，而这些操作的计算量都非常大。在比特币网络中，每个节点都要验证每一笔交易，所以当你在网络中发出一笔交易时，全网几千个节点都要验证你的签名。因此，即使签名的过程开销变得更大，让验证签名变得更简单也还是非常有好处的。其次，节点在验证签名时，每个签名都要单独验证。在一个m-n的多签交易中，节点必须多次验证同一个签名。比如一笔7-11的多签名交易，里面包含了7个签名，网络中的每个节点都要分别验证7个签名。另外，这种交易的体积也非常大，用户必须为此付出多得多的手续费。Schnorr签名

巨鲸地址将3000万USDT转入Binance后提币17,929枚ETH:6月17日消息，据链上分析师余烬监测，某巨鲸地址昨日今日两天内共计将3000万枚USDT转入Binance后提币17,929枚ETH，买入均价约为1673美元。

据悉，该地址曾于2022年6月至10月期间从CEX提币50,152枚ETH，此后于今年3月16日将ETH再次转入Binance并提币8522万枚USDT，出售均价约为1700美元。[2023/6/18 21:44:28]

Schnorr签名的生成方式有些许不同。它不是两个标量(r,s)，而是一个点R和一个标量s。类似于ECDSA签名，R是一个椭圆曲线上的随机点R=k*G。而签名的第二部分s的计算过程也有一些不同：s=k+hash(P,R,m)?pk。这里pk就是你的私钥，而P=pk*G是你的公钥，m就是那条消息。验证过程是检查s*G=R+hash(P,R,m)*P。

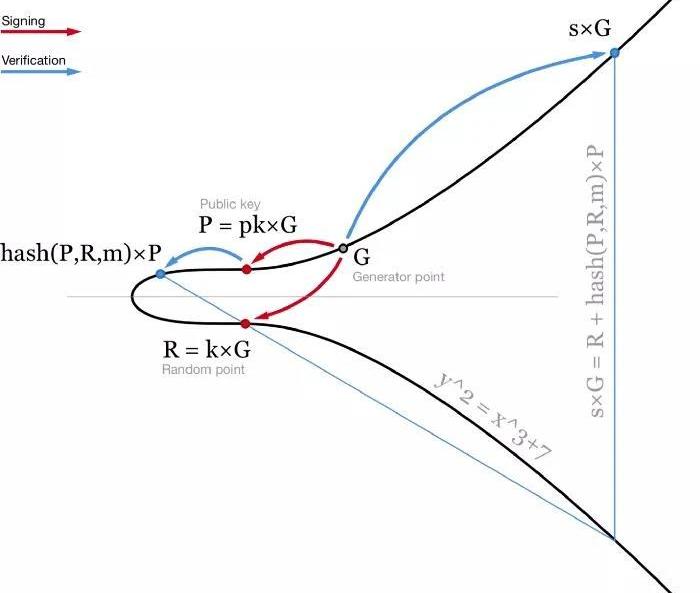
-图解Schnorr签名和验证-这个等式是线性的，所以多个等式可以相加相减而等号仍然成立。这给我们带来了Schnorr签名的多种良好特性。1.批量验证

Bitmex首席执行官Alexander H?ptner宣布辞职:金色财经报道，Alexander H?ptner 将立即辞去加密交易所 Bitmex 首席执行官的职务。H?ptner 于 2021 年 1 月加入 Bitmex。Stephan Lutz 已被任命为临时首席执行官。[2022/10/25 16:38:24]

在验证区块链上的一个区块时，我们需要验证区块中所有交易的签名都是有效的。如果其中一个是无效的，无论是哪一个——我们都必须拒绝掉整个区块。ECDSA的每一个签名都必须专门验证，意味着如果一个区块中包含1000条签名，那我们就需要计算1000次除法和2000次点乘法，总计约3000次繁重的运算。但有了Schnorr签名，我们可以把所有的签名验证等式加起来并节省一些计算量。在一个包含1000笔交易的区块中，我们可以验证：(s1+s2+…+s1000)×G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)这里就是一连串的点加法和1001次点乘法。已经是几乎3倍的性能提升了——验证时只需为每个签名付出一次重运算。

预警：“中国香港数字交易中心”发布“蔚来币”系虚假信息，请谨防风险:7月21日消息，名为“中国香港数字交易中心”的平台在其官网发布有关“蔚来币（NIO）全球首次发行以及申购指南”的虚假公告，经求证与蔚来汽车毫无关系，请用户注意甄别，防范相关风险。[2022/7/21 2:27:57]

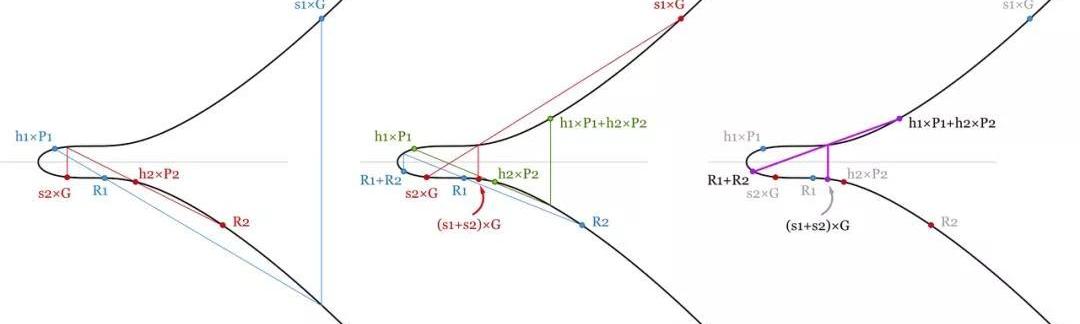
-两个签名的批量验证。因为验证等式是线性可加的，所以只要所有的签名都是有效的，这几个等式的和等式也必成立。我们节约了一些运算量，因为标量和点加法比点乘法容易计算得多。-2.密钥生成

我们想要安全地保管自己的比特币，所以我们可能会希望使用至少两把不同的私钥来控制比特币。一个在笔记本电脑或者手机上使用，而另一个放在硬件钱包/冷钱包里面。即使其中一个泄露了，我们还是掌控着自己的比特币。当前，实现这种钱包的做法是通过2-2的多签名脚本。也就是一笔交易需要包含两个独立的签名。有了Schnorr签名，我们可以使用一对密钥(pk1,pk2)，并使用一个共享公钥P=P1+P2=pk1*G+pk2*G生成一个共同签名。在生成签名时，我们需要在两个设备上分别生成一个随机数，并以此生成两个随机点Ri=ki*G，再分别加上hash(P,R1+R2,m)，就可以获得s1和s2了。最后，把它们都加起来即可获得签名(R,s)=(R1+R2,s1+s2)，这就是我们的共享签名，可用共享公钥来验证。其他人根本无法看出这是不是一个聚合签名，它跟一个普通的Schnorr签名看起来没有两样。不过，这种做法有三个问题。第一个问题是UI上的。要发起一笔交易，我们需要在两个设备上发起多轮交互——为了计算共同的R，为了签名。在两把私钥的情况下，只需访问一次冷钱包：我们可以在热钱包里准备好待签名的交易，选好k1并生成R1=k1*G，然后把待签名的交易和这些数据一同传入冷钱包并签名。因为已经有了R1，签名交易在冷钱包中只需一轮就可以完成。从冷钱包中我们得到R2和s2，传回给热钱包。热钱包使用前述的签名交易，把两个签名加总起来即可向外广播交易了。这在体验上跟我们现在能做到的没有什么区别，而且每当你加多一把私钥，问题就会变得更加复杂。假设你有一笔财富是用10把私钥共同控制的，而10把私钥分别存放在世界各地，这时候你要发送交易，该有多麻烦！在当前的ECDSA算法中，每个设备你都只需要访问一次，但如果你用上Schnorr的密钥聚合，则需要两次，以获得所有的Ri并签名。在这种情况下，可能不使用聚合，而使用各私钥单独签名的方式会好一些——这样就只需要一轮交互。文章完成后，我得到了ManuDrijvers的反馈：在一个可证明安全性的多签名方案中，你需要3轮交互：选择一个随机数ki以及相应的随机点Ri=ki\\G，然后告诉每一个设备Ri的哈希值ti=hash(Ri)，然后每个设备都能确保你没有在知道其他人的随机数之后改变主意*收集所有的数字Ri并计算公共的R签名第二个问题是已知的Rogue密钥攻击。这篇论文讲解得非常好，所以我就不赘述了。大概意思是如果你的其中一个设备被黑，并假装自己的公钥是，那就可以仅凭私钥pk1便控制两个私钥共享的资金。一个简单的解决方案是，在设置设备时，要求使用私钥对相应的公钥签名。还有第三个重大问题。你没法使用确定性的k来签名。如果你使用了确定性的k，则只需一种简单的攻击，黑客即可获得你的私钥。攻击如下：某个黑客黑入你的笔记本电脑，完全控制了其中一把私钥。我们感觉资金仍是安全的，因为使用我们的比特币需要pk1和pk2的聚合签名。所以我们像往常一样发起交易，准备好一笔待签名的交易和R1，发送给我们的硬件钱包，硬件钱包签名后将发回给热钱包……然后，热钱包出错了，没法完成签名和广播。于是我们再试一次，但这一次被黑的电脑用了另一个随机数——R1'。我们在硬件钱包里签名了同一笔交易，又将发回给了被黑的电脑。这一次，没有下文了——我们所有的比特币都不翼而飞了。在这次攻击中，黑客获得了同一笔交易的两个有效的签名：和。这个R2是一样的，但是R=R1+R2和R'=R1'+R2是不同的。这就意味着黑客可以计算出我们的第二个私钥：s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))?pk2或者说pk2=(s2-s2')/(hash(P,R1+R2,m)-hash(P,R1'+R2,m))。我发现这就是密钥聚合最不方便的地方——我们每次都要使用一个好的随机数生成器，这样才能安全地聚合。3.Musig

Solana官方：网络运营商和 dapp 将在接下来的几个小时内恢复客户服务:金色财经报道，Solana官方发推称，今天早些时候，当节点为同一块生成不同的结果时，持久随机数交易功能中的一个错误导致了不确定性，从而阻止了网络的发展。在网络未能达成共识后大约 4 个半小时的中断之后，验证者运营商在 UTC 晚上 9:00 成功完成了 Mainnet Beta 的集群重启。网络运营商和 dapp 将在接下来的几个小时内继续恢复客户服务。主网测试版验证者请按照下面链接的重启说明，将1.9.x升级到1.9.28，如果你版本是1.10.x，请升级到1.10.23。[2022/6/2 3:57:22]

MuSig解决了其中一个问题——roguekey攻击将不能再奏效。这里的目标是把多方/多个设置的签名和公钥聚合在一起，但又无需你证明自己具有与这些公钥相对应的私钥。聚合签名对应着聚合公钥。但在MuSig中，我们不是把所有联合签名者的公钥直接相加，而是都乘以一些参数，使得聚合公钥P=hash(L,P1)×P1+…+hash(L,Pn)×Pn。在这里，L=hash(P1,…,Pn)——这个公共数基于所有的公钥。L的非线性特性阻止了攻击者构造特殊的公钥来发动攻击。即使攻击者知道他的hash(L,Patk)×Patk应该是什么，他也无法从中推导出Patk来——这就跟你想从公钥中推导出私钥是一样的。签名构造的其它过程跟上面介绍的很像。在生成签名时，每个联合签名者都选择一个随机数ki并与他人分享Ri=ki*G。然后他们把所有的随机点加起来获得R=R1+…+Rn，然后生成签名si=ki+hash(P,R,m)?hash(L,Pi)?pki。因此，聚合签名是(R,s)=(R1+…+Rn,s1+…+sn)，而验证签名的方法与以前一样：s×G=R+hash(P,R,m)×P。4.默克尔树多签名

报告：沙特阿拉伯探索在政府中实施区块链的可能性:金色财经报道，一份报告援引一位政府官员的话说，沙特阿拉伯正在考虑在该国使用加密货币以及对区块链采取行动。此外，该报告称，沙特还一直在讨论 Web3 技术以及如何利用这些技术。尽管如此，Unlock Media 的一份报告中引用了内政部长助理Prince Bandar Bin Abdullah Al Mishari的话说，他表示，在沙特阿拉伯成功建立基于区块链的解决方案之前，还需要做更多的工作。他说：已经有几次会议和网络研讨会讨论了区块链在政府中的实施，但在我看来，所有这些研究和法规都无法在区块链上构建解决方案，除非我们在这些实体中拥有能够利用区块链开发解决方案的创新人才， Web3 和加密货币。

虽然沙特政府尚未就加密货币的使用做出决定，但最近的一项调查表明，该国一半以上的居民认为应该使用数字货币进行支付。[2022/4/24 14:44:17]

你可能也注意到了，MuSig和密钥聚合需要*所有签名者签名一个交易*。但如果你想做的是2-3的多签名脚本呢？这时候我们能够使用签名聚合吗，还是不得不使用通常的OP_CHECKMULTISIG和分别签名？先说答案，是可以的，但是协议上将有些许的不同。我们可以开发一个类似于OP_CHECKMULTISIG的操作码，只不过是检查聚合签名是否对应于公钥默克尔树上的一个元素。举个例子，如果我们想用公钥P1、P2和P3组成一个2-3的多签名脚本，我们需要用这几把公钥的所有两两组合、、来构建一棵默克尔树，并把默克尔树根公布在锁定脚本中。在花费比特币时，我们需要提交一个签名和一个证据，证明这个签名所对应的公钥位于由这个树根标记的默克尔树上。对于2-3多签名合约来说，树上只有3个元素，证据只需2条哈希值——那个我们想用的公钥组合的哈希值，还有一个邻居的。对于7-11多签名脚本来说，公钥组合有11!/7!/4!=330种，证据需要8条哈希值。通常来说，证据所包含的元素数量与多签名的密钥数量大体成正比，为log2(n!/m!/(n-m))。但有了默克尔公钥树，我们就不必局限于m-n多签名脚本了。我们可以做一棵使用任意公钥组合的树。举个例子，如果我们有一个笔记本电脑，一个手机，一个硬件钱包和一个助记词，我们可以构建一棵默克尔树，允许我们使用笔记本电脑+硬件钱包、手机+硬件钱包或者单独的助记词来使用比特币。这是当前的OP_CHECKMULTISIG做不到的——除非你使用“IF-Else”式的流程控制来构造更复杂的脚本。

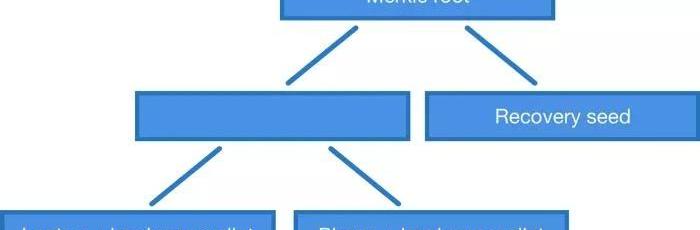
-聚合公钥的默克尔树。不仅仅是多签名-结论

Schnorr签名很棒，它解决了区块验证中的一些计算开销问题，也给了我们密钥聚合的能力。后者在使用时有些不便利，但我们不是在强迫大家使用它——无论如何，我们都可以仍旧使用普通的多签名方案，使用单独的、不聚合的签名。我迫不及待想使用Schnorr签名，希望比特币协议能尽快纳入这种签名方案。另外，我也真心喜欢MuSig，它是个优雅的方案，论文也浅显易懂。我强烈建议各位有闲之时通读全文。

标签：ASHHASH比特币SCHELCASH币metahash比特币官方cumuluschain

ADA热门资讯